|
| View previous topic :: View next topic |
| Author |
Message |
Furan
Joined: 05 Oct 2010
Posts: 64
Location: Prague, Czech Republic
|
 Posted: Thu May 16, 2013 11:26 am Post subject: Posted: Thu May 16, 2013 11:26 am Post subject: |
 |
|
I'm afraid you made an error in there.
I don't even recognize where that alpha is comming from.
a=edge length
GoldenRatio phi=(1+sqrt(5))/2
Let's look at the top pyramid of 5 triangles:
Circle circumscribed onto its base:
R = sqrt((5+sqrt(5))/10) * a = sqrt((2+phi)/5) * a
Circle inscribed in its base
r = sqrt((5+2*sqrt(5))/20) * a = sqrt((3+4*phi)/20) * a
In your case, alpha is the angle of the face normal from the z-axis,
that is cos(alpha) = r/v; v = sqrt(3)/2 * a = triangle height
cos(alpha) = sqrt((5+2*sqrt(5)/15) = sqrt((3+4*phi)/15) = 0.79465
sin(alpha) = sqrt((10-2*sqrt(5)/15) = sqrt((12-4*phi)/15) = 0.60706
Now let's look at the 10 triangles in the middle row:
cos(beta) = (R-r) / v = 0.18759
sin(beta) = 1-cos^2(beta) = 0.98225
So the number you were looking for is beta = 1.382086 rad |
|
| Back to top |
   |
 |
abdelhamid belaid
Joined: 13 Aug 2009
Posts: 170
|
 Posted: Thu May 16, 2013 10:24 pm Post subject: Posted: Thu May 16, 2013 10:24 pm Post subject: |
 |
|
Hello my best friends, thanks Gerd, thanks Furan,
I would like to add (another method):
firstly, for the first angle, according to my calculations it is P=0.652358
for the second angle Gerd asked about, this is a method where we won't use the golden ratio:
let A , B , C , D are four vertices as shown on the first picture down, let alpha is the angle made by the vectors OA and OB (or by the origin and any two other vertices for the same edge),
the equation of the plane ABC is x*sin(P) + z*cos(P) + c = 0
we have:
A(0 , 0 , h)
B(h*sin(alpha)*cos(pi/5) , h*sin(alpha)*sin(pi/5) , h*cos(alpha))
C(h*sin(alpha)*cos(pi/5) , -h*sin(alpha)*sin(pi/5) , h*cos(alpha))
D(h*sin(alpha) , 0 , -h*cos(alpha))
A belongs to ABC, that means 0*sin(P) + h*cos(P) + c = 0 so c= - h*cos(P)
so the ABC equation becomes x*sin(P) + z*cos(P) - h*cos(P) = 0
now let's calculate alpha, since B belongs to ABC we have
h*sin(alpha)*cos(pi/5)*sin(P) + h*cos(alpha)*cos(P) - h*cos(P) = 0
so sin(alpha)*cos(pi/5)*sin(P) + cos(alpha)*cos(P) - cos(P) = 0
here is alpha = 1.107148 (I call it the golden angle)
finally we can calculate "u" an orthogonal vector for the BCD plane and then calculate the second angle T = arccos(u*k / ||u||)
we can also using "E" the middle of BC, in this case T = 2*(OE , k) - P
also we can use "G" the centroid of the triangle BCD, here is T = (OG , k)
also we can directly write the BCD plane equation, we have but to solve a system of equations: (a*xB+b*yB+c*zB+1=0 , a*xC+b*yC+c*zC+1=0 , a*xD+b*yD+c*zD+1=0) , there are many other methods in fact.


_________________
My YouTube channel
Last edited by abdelhamid belaid on Fri May 17, 2013 11:16 am; edited 1 time in total |
|
| Back to top |
    |
 |
abdelhamid belaid
Joined: 13 Aug 2009
Posts: 170
|
 Posted: Fri May 17, 2013 1:07 am Post subject: Posted: Fri May 17, 2013 1:07 am Post subject: |
 |
|
I must add, I have made a tiny mistake when writing my dodecahedron formulas, the angle I should write is alpha = 1.107148 instead of 1.07498, I'm sorry.
| Code: | Name: AB_dodecahedron
F(): max(max(
sin(1.107148)*sqrt(x*x+y*y)*cos(atan(tan(2.5*atan2(y,x)))/2.5)+cos(1.107148)*z
,
sin(1.107148)*sqrt(x*x+y*y)*cos(atan(tan(2.5*(atan2(y,x)+pi/5)))/2.5)-cos(1.107148)*z )
,
abs(z) )- 3
[x]: -3.8 , 3.8
[y]: -3.6 , 3.6
[z]: -3.1 , 3.1
; |

_________________
My YouTube channel
Last edited by abdelhamid belaid on Sat May 18, 2013 8:54 pm; edited 1 time in total |
|
| Back to top |
    |
 |
abdelhamid belaid
Joined: 13 Aug 2009
Posts: 170
|
 Posted: Fri May 17, 2013 1:35 am Post subject: Posted: Fri May 17, 2013 1:35 am Post subject: |
 |
|
I have one more question, as you see we didn't talk about the first angle P, how would us calculate it ? I mean I want to restore our issues to their origins, in our methods we have used known values (I used P and Furan used the golden ratio), how could us calculate P or the golden ratio?
if we have alpha we can easily get P, so how would us calculate alpha? I mean here we need to return to the basic definition of the icosahedron or the dodecahedron ? what are they ? 
_________________
My YouTube channel |
|
| Back to top |
    |
 |
inode

Joined: 27 Jan 2007
Posts: 127
Location: Austria
|
 Posted: Mon May 20, 2013 12:52 pm Post subject: touching balls Posted: Mon May 20, 2013 12:52 pm Post subject: touching balls |
 |
|
| Quote: | abdelhamid belaid wrote...
I must add, ... alpha = 1.107148 instead of 1.07498. |
Hi all
Using alpha = 1.107148 seems to be the right angle. Rearranging the formula result in 12 touching balls. There you can compare the empty space between the spheres visually. All the holes looks equal now!
| Code: | /* Isosurface: PG_DodecaBalls1 5/2013
12 Touching Balls at dodecahedron polygon middle points */
max(max(
sin(1.107148) *sqrt(x*x+y*y) *cos(atan(tan(2.5* atan2(y,x) ))/2.5)+cos(1.107148)*z
,sin(1.107148) *sqrt(x*x+y*y) *cos(atan(tan(2.5*(atan2(y,x)+pi/5)))/2.5) -cos(1.107148)*z )
,abs(z))
-(x*x+y*y+z*z) -0.177
|
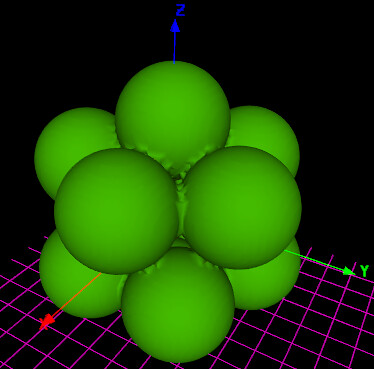
 Gerd Gerd |
|
| Back to top |
  |
 |
abdelhamid belaid
Joined: 13 Aug 2009
Posts: 170
|
 Posted: Mon May 20, 2013 11:15 pm Post subject: Posted: Mon May 20, 2013 11:15 pm Post subject: |
 |
|
very nice, Gerd 
some variations:
| Code: | Name: AB_dodecahedron7
F(): max(max(
sin(1.107148) *sqrt(x*x+y*y) *cos(atan(tan(2.5* atan2(y,x) ))/2.5)+cos(1.107148)*z
,sin(1.107148) *sqrt(x*x+y*y) *cos(atan(tan(2.5*(atan2(y,x)+pi/5)))/2.5) -cos(1.107148)*z )
,abs(z))
-(x*x+y*y+z*z)
[x]: -2 , 2
[y]: -2 , 2
[z]: -2 , 2
; |

| Code: | Name: AB_dodecahedron8
F(): max(max(
sin(1.107148) *sqrt(x*x+y*y) *cos(atan(tan(2.5* atan2(y,x) ))/2.5)+cos(1.107148)*z
,sin(1.107148) *sqrt(x*x+y*y) *cos(atan(tan(2.5*(atan2(y,x)+pi/5)))/2.5) -cos(1.107148)*z )
,abs(z))^3
-(x*x+y*y+z*z)
[x]: -2 , 2
[y]: -2 , 2
[z]: -2 , 2
; |

| Code: | Name: AB_dodecahedron9
F(): (max(max(
sin(1.107148) *sqrt(x*x+y*y) *cos(atan(tan(2.5* atan2(y,x) ))/2.5)+cos(1.107148)*z
,sin(1.107148) *sqrt(x*x+y*y) *cos(atan(tan(2.5*(atan2(y,x)+pi/5)))/2.5) -cos(1.107148)*z )
,abs(z) )+0.18)^3
-(x*x+y*y+z*z)
[x]: -1.2 , 1.2
[y]: -1.2 , 1.2
[z]: -1.2 , 1.2
; |

| Code: | Name: AB_dodecahedron10
F(): (max(max(
sin(1.107148) *sqrt(x*x+y*y) *cos(atan(tan(2.5* atan2(y,x) ))/2.5)+cos(1.107148)*z
,sin(1.107148) *sqrt(x*x+y*y) *cos(atan(tan(2.5*(atan2(y,x)+pi/5)))/2.5) -cos(1.107148)*z )
,abs(z) )+0.2)^3
-(x*x+y*y+z*z)
[x]: -1 , 1
[y]: -1 , 1
[z]: -1 , 1
; |

_________________
My YouTube channel |
|
| Back to top |
    |
 |
denisc
Joined: 24 Apr 2013
Posts: 92
|
 Posted: Thu May 23, 2013 11:34 pm Post subject: Posted: Thu May 23, 2013 11:34 pm Post subject: |
 |
|
thanks very much
AB_dodecahedron8
look like hyperbolic dodecaedron !
i find that a lot of time.

with more points on top perhaps
denisc |
|
| Back to top |
   |
 |
abdelhamid belaid
Joined: 13 Aug 2009
Posts: 170
|
 Posted: Tue Jun 25, 2013 10:17 pm Post subject: Posted: Tue Jun 25, 2013 10:17 pm Post subject: |
 |
|
thanks Denis,
anyway it's an old work, let's break the silence 

_________________
My YouTube channel |
|
| Back to top |
    |
 |
Furan
Joined: 05 Oct 2010
Posts: 64
Location: Prague, Czech Republic
|
 Posted: Tue Jun 25, 2013 10:56 pm Post subject: Posted: Tue Jun 25, 2013 10:56 pm Post subject: |
 |
|
Exquisite ! Made my head spin 
Anyway, how fine can you make the grid? Could you apply a uniform transformation for that (I posted it here somewhere for the hexgrid toroid) with all the features visible? The features closer to center would get really tiny. Or are there any such options when exporting mesh to POVray?
I'm struggling with the same problem with the software that I use. I tried matlab and it was promissing. I managed to visualise much finer grids.
Speaking of matlab, this is just a teaser of what I did recently (actually a real science for a change):

Once I finish this research, I will create more realistic equations of knitwear. |
|
| Back to top |
   |
 |
denisc
Joined: 24 Apr 2013
Posts: 92
|
 Posted: Fri Sep 12, 2014 9:56 am Post subject: Posted: Fri Sep 12, 2014 9:56 am Post subject: |
 |
|
hello
thanks for your help. |
|
| Back to top |
   |
 |
|
|
You cannot post new topics in this forum
You cannot reply to topics in this forum
You cannot edit your posts in this forum
You cannot delete your posts in this forum
You cannot vote in polls in this forum
|
2005 Powered by phpBB © 2001, 2005 phpBB Group
|