|
| View previous topic :: View next topic |
| Author |
Message |
abdelhamid belaid
Joined: 13 Aug 2009
Posts: 170
|
 Posted: Thu Jul 19, 2012 2:01 pm Post subject: Posted: Thu Jul 19, 2012 2:01 pm Post subject: |
 |
|
sure Gerd I do, try this 
| Code: | min(max( abs(y-floor(y/(2*cos(pi/6))+0.5)*(2*cos(pi/6)))-cos(pi/6) , abs(x-3*floor(x/3+0.5))*cos(pi/6)+abs(y-floor(y/(2*cos(pi/6))+0.5)*(2*cos(pi/6)))*sin(pi/6) -cos(pi/6) )^2,max( abs((y-cos(pi/6))-floor((y-cos(pi/6))/(2*cos(pi/6))+0.5)*(2*cos(pi/6)))-cos(pi/6) , abs((x-1.5)-3*floor((x-1.5)/3+0.5))*cos(pi/6)+abs((y-cos(pi/6))-floor((y-cos(pi/6))/(2*cos(pi/6))+0.5)*(2*cos(pi/6)))*sin(pi/6) -cos(pi/6) )^2 )+z^2-0.04
[x]: -4.5 , 4.5
[y]: -4 , 4
[z]: -0.3 , 0.3 |

_________________
My YouTube channel |
|
| Back to top |
    |
 |
abdelhamid belaid
Joined: 13 Aug 2009
Posts: 170
|
 Posted: Mon Jul 23, 2012 5:55 pm Post subject: Posted: Mon Jul 23, 2012 5:55 pm Post subject: |
 |
|
this is a much more better formula 
| Code: | min(max(abs(y-floor(y/2+0.5)*2),abs(x-3/cos(pi/6)*floor(x/3*cos(pi/6)+0.5))*cos(pi/6)+abs(y-floor(y/2+0.5)*2)*sin(pi/6))-1,abs(y-floor(y/2+0.5)*2))^2+z^2-0.0225
[x]: -5 , 5
[y]: -4.5 , 4.5
[z]: -0.5 , 0.5 |

generally write:
| Code: | | F( min(max(abs(y-floor(y/2+0.5)*2),abs(x-3/cos(pi/6)*floor(x/3*cos(pi/6)+0.5))*cos(pi/6)+abs(y-floor(y/2+0.5)*2)*sin(pi/6))-1,abs(y-floor(y/2+0.5)*2)) , z)=0 |
for example:
| Code: | abs(min(max(abs(y-floor(y/2+0.5)*2),abs(x-3/cos(pi/6)*floor(x/3*cos(pi/6)+0.5))*cos(pi/6)+abs(y-floor(y/2+0.5)*2)*sin(pi/6))-1,abs(y-floor(y/2+0.5)*2)) )+abs(z)-0.2
[x]: -5 , 5
[y]: -4.5 , 4.5
[z]: -0.2 , 0.2 |

also:
| Code: | (5*min(max(abs(y-floor(y/2+0.5)*2),abs(x-3/cos(pi/6)*floor(x/3*cos(pi/6)+0.5))*cos(pi/6)+abs(y-floor(y/2+0.5)*2)*sin(pi/6))-1,abs(y-floor(y/2+0.5)*2)))^2+(5*z)^20-1
[x]: -5 , 5
[y]: -4.5 , 4.5
[z]: -0.2 , 0.2 |

_________________
My YouTube channel |
|
| Back to top |
    |
 |
abdelhamid belaid
Joined: 13 Aug 2009
Posts: 170
|
 Posted: Fri Aug 24, 2012 11:53 am Post subject: Posted: Fri Aug 24, 2012 11:53 am Post subject: |
 |
|
Hi, this is the same but without min and max functions 
| Code: | (((abs(y-floor(y/2+0.5)*2)+ abs(x-3/cos(pi/6)*floor(x/3*cos(pi/6)+0.5))*cos(pi/6)+abs(y-floor(y/2+0.5)*2)*sin(pi/6)+abs(abs(y-floor(y/2+0.5)*2) - (abs(x-3/cos(pi/6)*floor(x/3*cos(pi/6)+0.5))*cos(pi/6)+abs(y-floor(y/2+0.5)*2)*sin(pi/6))))/2-1 +abs(y-floor(y/2+0.5)*2) -abs(( abs(y-floor(y/2+0.5)*2) +abs(x-3/cos(pi/6)*floor(x/3*cos(pi/6)+0.5))*cos(pi/6)+abs(y-floor(y/2+0.5)*2)*sin(pi/6) +abs( abs(y-floor(y/2+0.5)*2) -(abs(x-3/cos(pi/6)*floor(x/3*cos(pi/6)+0.5))*cos(pi/6)+abs(y-floor(y/2+0.5)*2)*sin(pi/6)) ))/2-1-abs(y-floor(y/2+0.5)*2)))/2)^2+z^2-0.04
[x]: -5.5 , 5.5
[y]: -6.5 , 6.5
[z]: -0.3 , 0.3 |

sure, generally you would write:
| Code: | | F( (((abs(y-floor(y/2+0.5)*2)+ abs(x-3/cos(pi/6)*floor(x/3*cos(pi/6)+0.5))*cos(pi/6)+abs(y-floor(y/2+0.5)*2)*sin(pi/6)+abs(abs(y-floor(y/2+0.5)*2) - (abs(x-3/cos(pi/6)*floor(x/3*cos(pi/6)+0.5))*cos(pi/6)+abs(y-floor(y/2+0.5)*2)*sin(pi/6))))/2-1 +abs(y-floor(y/2+0.5)*2) -abs(( abs(y-floor(y/2+0.5)*2) +abs(x-3/cos(pi/6)*floor(x/3*cos(pi/6)+0.5))*cos(pi/6)+abs(y-floor(y/2+0.5)*2)*sin(pi/6) +abs( abs(y-floor(y/2+0.5)*2) -(abs(x-3/cos(pi/6)*floor(x/3*cos(pi/6)+0.5))*cos(pi/6)+abs(y-floor(y/2+0.5)*2)*sin(pi/6)) ))/2-1-abs(y-floor(y/2+0.5)*2)))/2) ,z)=0 |
_________________
My YouTube channel |
|
| Back to top |
    |
 |
abdelhamid belaid
Joined: 13 Aug 2009
Posts: 170
|
 Posted: Mon Oct 29, 2012 9:36 pm Post subject: Posted: Mon Oct 29, 2012 9:36 pm Post subject: |
 |
|
Hello all,
I missed math and k3dsurf, is there anyone else like me?  also this is the same but this time without "floor" function also this is the same but this time without "floor" function 
| Code: | min(abs(abs(abs(abs(abs(abs(y)-16*cos(pi/6))-8*cos(pi/6))-4*cos(pi/6))-2*cos(pi/6))-cos(pi/6)),max( abs(abs(abs(abs(abs(abs(y)-16*cos(pi/6))-8*cos(pi/6))-4*cos(pi/6))-2*cos(pi/6))-cos(pi/6)), abs(abs(abs(abs(abs(x)-12)-6)-3)-1.5)*cos(pi/6)+abs(abs(abs(abs(abs(abs(y)-16*cos(pi/6))-8*cos(pi/6))-4*cos(pi/6))-2*cos(pi/6))-cos(pi/6))*sin(pi/6) )-cos(pi/6))^2+z^2-0.04
[x]: -6 , 6
[y]: -6 , 6
[z]: -0.7 , 0.7 |

_________________
My YouTube channel |
|
| Back to top |
    |
 |
abdelhamid belaid
Joined: 13 Aug 2009
Posts: 170
|
 Posted: Fri Nov 09, 2012 11:03 pm Post subject: Posted: Fri Nov 09, 2012 11:03 pm Post subject: |
 |
|
also, another formula for the same isosurface, I have no idea what k3dsurf could do recently, I have very silent friends on this forum 
| Code: | min(max(abs(2/pi*atan(tan(pi/2*y)))-1,abs(2/pi*atan(tan(pi/2*y)))*cos(pi/3)-(-abs(3/cos(pi/6)/pi*atan(tan(pi*x/3*cos(pi/6))))+1/cos(pi/6))*sin(pi/3)),abs(2/pi*atan(tan(pi/2*y))))^2+z^2-0.04
[x]: -5.5 , 5.5
[y]: -6.3 , 6.3
[z]: -0.4 , 0.4 |

_________________
My YouTube channel |
|
| Back to top |
    |
 |
Furan
Joined: 05 Oct 2010
Posts: 64
Location: Prague, Czech Republic
|
 Posted: Fri Feb 15, 2013 6:38 pm Post subject: HexGrid Donut Posted: Fri Feb 15, 2013 6:38 pm Post subject: HexGrid Donut |
 |
|
Sorry for being away for so long, I've been hanging around mainly at fractalforums.com Now I'm ready to fuse these two parts of my life together  I have an insane idea that I'm working on, it's gonna be awesome I have an insane idea that I'm working on, it's gonna be awesome 
Anyway, this is a toroid (R=2, r=1) made with my hexagonal grid with constant relative grid ratio:
| Code: | Transformation to local orthogonal system with distortion (usable to any other repeating pattern on this toroid)
x1=atan2(y,x)*8
y1=(atan2(z,(sqrt(x^2+y^2)-2)))*8/sqrt(x^2+y^2)
z1=((sqrt(x^2+y^2)-2)^2+z^2-1)*4/sqrt(x^2+y^2)
Good old hexagonal grid:
F=0.25+2*z1^2+(0.25*(cos(4*y1)+cos(2*sqrt(3)*x1-2*y1)+cos(2*sqrt(3)*x1+2*y1))+0.03*(cos(4*sqrt(3)*x1)+cos(6*y1-2*sqrt(3)*x1)+cos(6*y1+2*sqrt(3)*x1))) = 0
Limits:
-3.1..3.1
-3.1..3.1
-1.1..1.1
|
I'm skeptical about the grid density, it's gonna need something like 500x500x200, probably more. |
|
| Back to top |
   |
 |
abdelhamid belaid
Joined: 13 Aug 2009
Posts: 170
|
 Posted: Sat Mar 16, 2013 6:17 pm Post subject: Posted: Sat Mar 16, 2013 6:17 pm Post subject: |
 |
|
Hi all,
I've made some changes to your formula Furan 
| Code: | 0.2/(1+2/(1+3*(atan2(abs(z),sqrt(x*x+y*y)-6)-pi)^2))+0.8*((( ((sqrt(x*x+y*y)-6)^2+z*z)-4))*4/sqrt(x*x+y*y))^2+(0.25*(cos(2*4*((atan2(z,(sqrt(x*x+y*y)-6)))*8/sqrt(x*x+y*y)))+cos(2*sqrt(3)*(atan2(y,x)*8)-4*((atan2(z,(sqrt(x*x+y*y)-6)))*8/sqrt(x*x+y*y)))+cos(2*sqrt(3)*(atan2(y,x)*8)+4*((atan2(z,(sqrt(x*x+y*y)-6)))*8/sqrt(x*x+y*y))))+0.03*(cos(4*sqrt(3)*(atan2(y,x)*8))+cos(6*2*((atan2(z,(sqrt(x*x+y*y)-6)))*8/sqrt(x*x+y*y))-2*sqrt(3)*(atan2(y,x)*8))+cos(6*2*((atan2(z,(sqrt(x*x+y*y)-6)))*8/sqrt(x*x+y*y))+2*sqrt(3)*(atan2(y,x)*8)))) =0
[x]: -8.5 , 8.5
[y]: -8.5 , 8.5
[z]: -4 , 4 |


We are eager to know your idea Furan, I think it's making 3d fractals by making patterns many times (making patterns over a surface, then making the same patterns over the new surface, then making the same patterns over the new surface, ......) 
_________________
My YouTube channel |
|
| Back to top |
    |
 |
inode

Joined: 27 Jan 2007
Posts: 127
Location: Austria
|
 Posted: Mon Mar 18, 2013 2:45 pm Post subject: Hexagonal Grid Torus Posted: Mon Mar 18, 2013 2:45 pm Post subject: Hexagonal Grid Torus |
 |
|
Hi all,
I was deriving the formula for a hexagonal grid torus too
and I got a simpler term. Here it is...

| Code: | Name: PG_HexaGridTorus1
/* Isosurface: PG_HexaGridTorus1 12/2012 Gerd Platl */
F(): -0.5
-44*(sqrt( (sqrt(x*x+y*y)-5)^2 +z*z)-2)^2
-cos( 48*atan2(y,x))
-cos(14*atan2(z,sqrt(x*x+y*y)-5) -24*atan2(y,x))
-cos(14*atan2(z,sqrt(x*x+y*y)-5) +24*atan2(y,x))
-0.12*( cos( 28*atan2(z,sqrt(x*x+y*y)-5))
+cos(24*atan2(y,x) -14*atan2(z,sqrt(x*x+y*y)-5))
+cos(24*atan2(y,x) +14*atan2(z,sqrt(x*x+y*y)-5))
)
[x]: -7.2 , 7.2
[y]: -7.2 , 7.2
[z]: -2.2 , 2.2
; |
Last edited by inode on Mon Mar 25, 2013 7:05 pm; edited 1 time in total |
|
| Back to top |
  |
 |
inode

Joined: 27 Jan 2007
Posts: 127
Location: Austria
|
 Posted: Mon Mar 18, 2013 2:54 pm Post subject: Hexagonal Grid Cylinder Posted: Mon Mar 18, 2013 2:54 pm Post subject: Hexagonal Grid Cylinder |
 |
|
Hi all,
I also was creating the formula for the hexagonal grid cylinder...

| Code: | Name: PG_HexaGridCylinder1
/* Isosurface: PG_HexaGridCylinder1 12/2012 Gerd Platl
coat formula taken from PG_HexaGrid1
4.04 is used to connect coat at 360°
4.04*2*sqrt(3) =~ 13.995 =~ 14.0
*/
F(): -0.5
-88*(sqrt(x*x+y*y)-2)^2
-cos( 8*z)
-cos(14*atan2(y,x) -4*z)
-cos(14*atan2(y,x) +4*z)
-0.12*( cos( 28*atan2(y,x))
+cos(12*z -14*atan2(y,x))
+cos(12*z +14*atan2(y,x)))
[x]: -2.1 , 2.1
[y]: -2.1 , 2.1
[z]: 0 , 5
; |
and a variation of it...
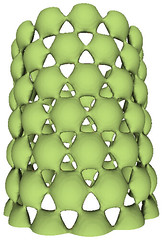
| Code: | Name: PG_HexaGridCylinder2
/* Isosurface: PG_HexaGridCylinder2 12/2012 Gerd Platl */
F(): 1.0
-88*(sqrt(x*x+y*y)-2)^2
-cos( 8*z)
-cos(14*atan2(y,x) -4*z)
-cos(14*atan2(y,x) +4*z)
- 0.12*( cos( 28*atan2(y,x))
+cos(12*z -14*atan2(y,x))
+cos(12*z +14*atan2(y,x)))
[x]: -2.3 , 2.3
[y]: -2.3 , 2.3
[z]: 0 , 5
; |
and a 2nd variation with imaginary circles build from the pillow elements...

| Code: | Name: PG_HexaGridCylinder3
/* Isosurface: PG_HexaGridCylinder3 12/2012 Gerd Platl */
F(): -0.55
-88*(sqrt(x*x+y*y)-2)^2
-cos( 8*z)
-cos(14*atan2(y,x) -4*z)
-cos(14*atan2(y,x) +4*z)
-0.6*( cos( 28*atan2(y,x))
+cos(12*z -14*atan2(y,x))
+cos(12*z +14*atan2(y,x)))
[x]: -2.2 , 2.2
[y]: -2.2 , 2.2
[z]: 0 , 5
; |
|
|
| Back to top |
  |
 |
abdelhamid belaid
Joined: 13 Aug 2009
Posts: 170
|
 Posted: Thu Apr 25, 2013 10:20 pm Post subject: Posted: Thu Apr 25, 2013 10:20 pm Post subject: |
 |
|
Hi all, it's just a crazy work you would say 
| Code: | F(): min(min(min( min( min( max(max( (sqrt(x^2+z^2)-1)^2+y^2-0.16,-x),-z),max(abs(x+1)-1,((x+1)^2+y^2+(z-1)^2-0.25)*(y^2+(z-1)^2-0.36)-0.03 )) ,max(sqrt((x-1)^2+y^2)-(0.65+min(-0.05,cos(30*atan2(y,(x-1)))/10) ) ,abs(3*(z+0.2))-1) ),max(max(abs(sqrt((x-1)^2+y^2)-0.35)-0.05,z+0.2),-(z+1.3)) ) ,min(min( max((x+1)^2+(z-2.5)^2-(0.2+0.1*abs(y))^2,abs(y)-0.5),(x+1)^2+y^2+(z-2.5)^2-0.0625 ) ,max(max((x+1)^2+y^2-0.0225,z-2.5),-(z-2.5+1.2)) ) ) ,max(y^2+(z-1)^2-0.25,x+1) )
[x]: -3.5 , 2.1
[y]: -1 , 1
[z]: -1.4 , 3
; |

_________________
My YouTube channel |
|
| Back to top |
    |
 |
denisc
Joined: 24 Apr 2013
Posts: 92
|
 Posted: Mon Apr 29, 2013 3:15 pm Post subject: Posted: Mon Apr 29, 2013 3:15 pm Post subject: |
 |
|
hello 
i am new .
thanks to all.
i am very impressive!!!
i don't know , it"s possible to wite min(min(min ect !
Can you explain, a little , how construct dodecaedron and icosaedron with
iso formula ? and also pentagon curve or solid pentagon
like a little of that :
( (abs(y)-1/(1+exp(7*(abs(x)-1))))*cos(atan(-7*exp(7*(abs(x)-1))
/(1+exp(7*(abs(x)-1)))^2)) )^2+z^2-0.04
i am very curious to understand that?
thanks in advance
cheers
denis |
|
| Back to top |
   |
 |
Furan
Joined: 05 Oct 2010
Posts: 64
Location: Prague, Czech Republic
|
 Posted: Tue Apr 30, 2013 11:08 am Post subject: Posted: Tue Apr 30, 2013 11:08 am Post subject: |
 |
|
I'd use something like this:
(Use different approach for tetrahedron.)
F(x,y,z) = max(f1,f2,...,fN)
N=3 for cube
N=6 for dodecahedron
N=10 for icosahedron
f1 = R - abs(X*n1)
f2 = R - abs(X*n2)
f3 = ...
where
X=[x,y,z]
R = half distance between opposite faces (radius of the inscribed sphere)
n_i = normal UNIT vector of one of the face of the i-th pair.
Start by calculating the normal vectors. You can find some help here:
http://en.wikipedia.org/wiki/Dodecahedron |
|
| Back to top |
   |
 |
denisc
Joined: 24 Apr 2013
Posts: 92
|
 Posted: Tue Apr 30, 2013 5:25 pm Post subject: Posted: Tue Apr 30, 2013 5:25 pm Post subject: |
 |
|
thank very much mr furan

it's not very easy to understand in one time.
i think it's near a same
abdelhamid belaid
formula for the Cube
Code:
max(max(abs(x),abs(y)),abs(y))-a =0
or in a mathematical writing: max(|x|,|y|,|z|)-a =0
i am a little trouble by the fact of max is the symbol of booleen intersection,
and i don't know , in final , where is a mathematical thinking and where is a 3D soft thinking specific language .
(it might be interesting to have more information or links for that)
when you write: x^2+y^2-1
the math language and soft is the same , and it"s easy
apart from that, I'll try to understand
cheers
den |
|
| Back to top |
   |
 |
denisc
Joined: 24 Apr 2013
Posts: 92
|
 Posted: Wed May 01, 2013 11:32 am Post subject: Posted: Wed May 01, 2013 11:32 am Post subject: |
 |
|
hello furan
what do you mean by
n_i = normal UNIT vector of one of the face of the i-th pair and ? and Start by calculating the normal vectors ?
the normal vector is calculate by/
|u|*|v|*sin of the angle ?
for dodecaedron
2*abs(2 /((1 + √5) / 2))*sin(arcos(-1/√5))
it's right?
in a begining, i supposed you mean length between 2 paire of faces?
another
it's impossible to write in k3d :
max(abs(1-x),abs(1-y),abs(1-z))
i suppose you mean
for the cube
max(max(abs(x),abs(y)),abs(z))
don't work
max(max(abs(x),abs(y)),abs(z))-1
work ?
for
N=3 for cube
X=[x,y,z]
but for
N=6 for dodecahedron
X=[x,y,z,?,?,?]
thanks for your help
denis |
|
| Back to top |
   |
 |
Furan
Joined: 05 Oct 2010
Posts: 64
Location: Prague, Czech Republic
|
 Posted: Wed May 01, 2013 9:42 pm Post subject: Posted: Wed May 01, 2013 9:42 pm Post subject: |
 |
|
I made a tiny mistake, sorry for that.
F(x,y,z) = min(f1,f2,...,fN)
Normal unit vector is orthogonal to the face surface
n = (nx ny nz)
You should be able to calculate it with a bit of trigonometry. If not, there is an easier way:
http://en.wikipedia.org/wiki/Dodecahedron
Let φ = (1 + √5) / 2 be the golden ratio.

Let us calculate the middle point of the side facing us as the geometric center of its 5 corners:
The pink vertex at [φ,0,-1/φ]
The orange vertices at [1,1,-1] and [1,-1,-1]
The green vertices at [0,1/φ,-φ] and [0,-1/φ,-φ]
middle point M = 1/5 * [2+φ,0,-1/φ-2-2*φ]
n1 = (M-[0, 0, 0])/norm(M-[0, 0, 0])
where norm(M-[0, 0, 0]) = Ri (radius of inscribed sphere)
For points as presented above,
Ri= 0.5*sqrt(5/2 + 11/2*sqrt(5))
n1 = 1/5 * [2+φ, 0, -1/φ-2-2*φ] / Ri
f_i = R - abs(n_i * X)
where R is the inscribed radius you want, X=[x,y,z]
You can start with the cube
R=1
n1 = (1, 0, 0)
n2 = (0, 1, 0)
n3 = (0, 0, 1)
=>
f1 = 1-abs(x)
f2 = 1-abs(y)
f3 = 1-abs(z)
F = min(f1,f2,f3)
It should work now. |
|
| Back to top |
   |
 |
|
|
You cannot post new topics in this forum
You cannot reply to topics in this forum
You cannot edit your posts in this forum
You cannot delete your posts in this forum
You cannot vote in polls in this forum
|
2005 Powered by phpBB © 2001, 2005 phpBB Group
|