| View previous topic :: View next topic |
| Author |
Message |
lopkiol
Joined: 26 Jan 2007
Posts: 20
Location: United Kingdom
|
 Posted: Fri Jan 26, 2007 7:32 pm Post subject: Periodic lattices Posted: Fri Jan 26, 2007 7:32 pm Post subject: Periodic lattices |
 |
|
These are 4 periodic lattices, with number of rods per node equal to 3, 4, 6 and 8. They come respectively from the Schwarz's surfaces G (Gyroid), D (Diamond), P (Plumber's nightmare) and W (Whatdoesitstandfor?).
Best at 60x60x60 grid resolution.
Enjoy the view. 
Compute x, y and z between -0.25*pi and 2.75*pi:
G: cos(x)*sin(y)+cos(y)*sin(z)+cos(z)*sin(x)+0.08*(cos(2*x)*cos(2*y)+cos(2*y)*cos(2*z)+cos(2*z)*cos(2*x))+1.47
D: sin(x)*sin(y)*sin(z)+sin(x)*cos(y)*cos(z)+cos(x)*sin(y)*cos(z)+cos(x)*cos(y)*sin(z)-0.07*(cos(4*x)+cos(4*y)+cos(4*z))+1.17
Compute x, y and z between 0 and 4*pi:
P: cos(x)+cos(y)+cos(z)+0.51*(cos(x)*cos(y)+cos(y)*cos(z)+cos(z)*cos(x))+1.47
W: cos(2*x)+cos(2*y)+cos(2*z)-1.95*(cos(x)*cos(y)+cos(y)*cos(z)+cos(z)*cos(x))+2.8 |
|
| Back to top |
  |
 |
nextstep
Site Admin
Joined: 06 Jan 2007
Posts: 539
|
 Posted: Fri Jan 26, 2007 10:06 pm Post subject: Re: Periodic lattices Posted: Fri Jan 26, 2007 10:06 pm Post subject: Re: Periodic lattices |
 |
|
| lopkiol wrote: | These are 4 periodic lattices, with number of rods per node equal to 3, 4, 6 and 8. They come respectively from the Schwarz's surfaces G (Gyroid), D (Diamond), P (Plumber's nightmare) and W (Whatdoesitstandfor?).
Best at 60x60x60 grid resolution.
Enjoy the view. 
|
waw lopkiol...really great structures 
An image of what lopkiol is talking about:

Taha
_________________
Cheers,
Abderrahman |
|
| Back to top |
  |
 |
lopkiol
Joined: 26 Jan 2007
Posts: 20
Location: United Kingdom
|
 Posted: Fri Feb 02, 2007 7:21 pm Post subject: Posted: Fri Feb 02, 2007 7:21 pm Post subject: |
 |
|
| Thanks Taha. How can I post an image I have on my HD? |
|
| Back to top |
  |
 |
nextstep
Site Admin
Joined: 06 Jan 2007
Posts: 539
|
 Posted: Sun Feb 04, 2007 5:48 am Post subject: Posted: Sun Feb 04, 2007 5:48 am Post subject: |
 |
|
Hi,
Try this link:
http://imagehost.bizhat.com/
I just discovered this free service 
Taha
_________________
Cheers,
Abderrahman |
|
| Back to top |
  |
 |
nextstep
Site Admin
Joined: 06 Jan 2007
Posts: 539
|
 Posted: Sun Feb 04, 2007 5:52 am Post subject: Posted: Sun Feb 04, 2007 5:52 am Post subject: |
 |
|
When you uploaded the image, look for the third code "Thumbnail for Forums - BB Code"
Test:

_________________
Cheers,
Abderrahman |
|
| Back to top |
  |
 |
lopkiol
Joined: 26 Jan 2007
Posts: 20
Location: United Kingdom
|
 Posted: Sun Feb 04, 2007 1:24 pm Post subject: Posted: Sun Feb 04, 2007 1:24 pm Post subject: |
 |
|
Great! This the skeletal graph of a gyroid between -1.75*pi and 2.25*pi. 
cos(x)*sin(y)+cos(y)*sin(z)+cos(z)*sin(x)+0.05*(cos(2*x)*cos(2*y)+cos(2*y)*cos(2*z)+cos(2*z)*cos(2*x))+1.4
 |
|
| Back to top |
  |
 |
nextstep
Site Admin
Joined: 06 Jan 2007
Posts: 539
|
 Posted: Sun Feb 04, 2007 4:39 pm Post subject: Posted: Sun Feb 04, 2007 4:39 pm Post subject: |
 |
|
Beautiful look and colors...quite surealistic!
Did they all belong to a familly of mathematical surfaces?
Taha
_________________
Cheers,
Abderrahman |
|
| Back to top |
  |
 |
lopkiol
Joined: 26 Jan 2007
Posts: 20
Location: United Kingdom
|
 Posted: Sun Feb 04, 2007 6:25 pm Post subject: Posted: Sun Feb 04, 2007 6:25 pm Post subject: |
 |
|
Yes, they are triply periodic trigonometric functions. It's quite easy to experiment with them, just try out a combination of sines and cosines paying attention to the symmetry of x, y and z. The most famous examples are already in K3DSurf.
Have a look to the Matematical Sciences Research Institute in Berkeley: http://www.msri.org/about/sgp/jim/geom/level/skeletal/index.html |
|
| Back to top |
  |
 |
lopkiol
Joined: 26 Jan 2007
Posts: 20
Location: United Kingdom
|
 Posted: Mon Feb 05, 2007 11:20 am Post subject: Posted: Mon Feb 05, 2007 11:20 am Post subject: |
 |
|
The problem with this kind of surfaces is that they are open on the sides. It would be useful to provide the program with some patch addition feature (on the boundaries, the bounding box) so that a closed volume could be defined.
This is a variable density gyroid generated via a small routine in C that include bounding patches generation. The model is used for bone microstructure modeling. The file was a gts (GNU Triangulated Surface Library) and it has been converted to an stl for the creation on an SLS (Selective Laser Sintering) machine.
I would like to show you the 3D but I need to know how. A VRML?
 |
|
| Back to top |
  |
 |
nextstep
Site Admin
Joined: 06 Jan 2007
Posts: 539
|
 Posted: Mon Feb 05, 2007 3:29 pm Post subject: Posted: Mon Feb 05, 2007 3:29 pm Post subject: |
 |
|
| lopkiol wrote: | The problem with this kind of surfaces is that they are open on the sides. It would be useful to provide the program with some patch addition feature (on the boundaries, the bounding box) so that a closed volume could be defined.
|
Hi,
Thanks for the link and for the model...very interesting use of mathematical models 
Boundaries could be closed by using some CSG transformations along with Isosurfaces formulas, so a closed volume can be defined: Example
cube - sphere : ( x^10 + y^10 + z^10 -1)* (x*x + y*y + z*z - 1) .
However, complicated formulas need some work. I'll try to post some examples later.
VRML is well supported by all web browsers so it should be great to visualise your model in 3D ( I'm planing in near future to make K3DSurf able to load some basic models in OBJ and VRML file format...)
_________________
Cheers,
Abderrahman |
|
| Back to top |
  |
 |
lopkiol
Joined: 26 Jan 2007
Posts: 20
Location: United Kingdom
|
 Posted: Mon Feb 05, 2007 7:37 pm Post subject: Posted: Mon Feb 05, 2007 7:37 pm Post subject: |
 |
|
Good idea! Let's try. I generate the surface (don't look at the background, it seems I was using 2 applications, but actually I don't know where the hell it comes from, it's probably Paint fault...  ): ):

I insert the smooth cube:

And cut out the crap with the CND (look at the values in red, I needed to reduce that number because it eats the surface otherwise):

Result: it seems to be alright, but a close look reveals holes in the patches...  |
|
| Back to top |
  |
 |
nextstep
Site Admin
Joined: 06 Jan 2007
Posts: 539
|
 Posted: Mon Feb 05, 2007 11:41 pm Post subject: Posted: Mon Feb 05, 2007 11:41 pm Post subject: |
 |
|
Try to use the "if" instructions like shown in this examples :
Schwartz + Cube : | Quote: |
F():if(
(x^10 + y^10 +z^10 < 100000), //Condition
(cos(x) + cos(y) + cos(z) ) , // Schwartz
- (x^10 + y^10 +z^10 - 100000) // Cube with the signe"-"
)
[x]:-4, 4 [y]:-4, 4 [z]:-4, 4 |

_________________
Cheers,
Abderrahman |
|
| Back to top |
  |
 |
jotero
Joined: 27 Jan 2007
Posts: 153
Location: Germany Hannover
|
 Posted: Tue Feb 06, 2007 7:56 am Post subject: Posted: Tue Feb 06, 2007 7:56 am Post subject: |
 |
|
my idea ;)
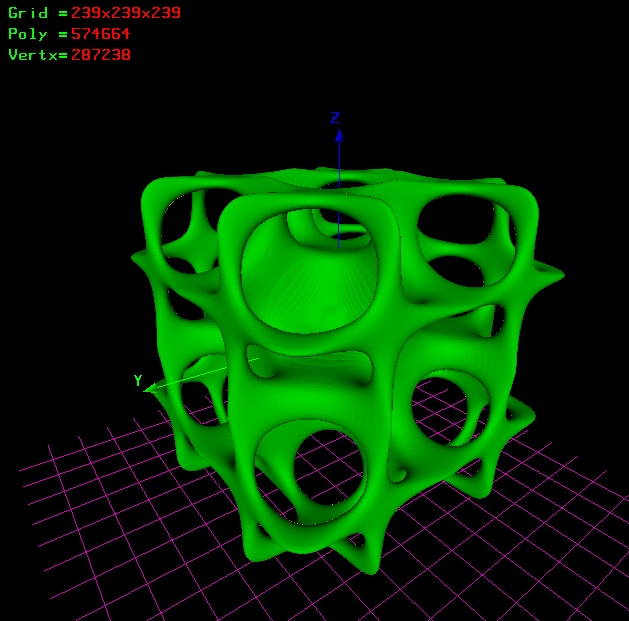
| Quote: | F():( x^10 + y^10 + z^10 -1)- ((1/10^5.2)^ (cos(2*x) * cos(2*y)+
cos(2*y) * cos(2*z)+ cos(2*z) * cos(2*x)))
[x]:-4.10, 4.10
[y]:-4.10, 4.10
[z]:-4.10, 4.10
|
ciao
torolf
_________________
Kontakte |
|
| Back to top |
     |
 |
lopkiol
Joined: 26 Jan 2007
Posts: 20
Location: United Kingdom
|
 Posted: Tue Feb 06, 2007 12:21 pm Post subject: Posted: Tue Feb 06, 2007 12:21 pm Post subject: |
 |
|
| nextstep wrote: | | Try to use the "if" instructions |
Perfect! That was the function I needed! I wanted parallel planes on the sides so I wrote this:
if((abs(x)<2*pi)&(abs(y)<2*pi)&(abs(z)<2*pi),cos(x)+cos(y)+cos(z)+0.53*(cos(x)*cos(y)+cos(y)*cos(z)+cos(z)*cos(x))+1.4,1)
with boundaries -2*pi and 2*pi.
I don't know why, but it works really well! 

The "else" field, as you can clearly see, is "1". This means 1=0, that is impossible. But it works... 
I noticed that I can also adjust the smoothness of the patches by varying this number between an arbitrary small positive number (curved)

to an arbitrary big one (flat).

I guess it is something that has to do with the resolution of the numbers in the computer, but the point is that I like it. 
Jotero, your structure is beautiful but I wanted to patch mine. How the hell can you go up to 239 of grid resolution?!?
ciao
Ruggero |
|
| Back to top |
  |
 |
jotero
Joined: 27 Jan 2007
Posts: 153
Location: Germany Hannover
|
 Posted: Tue Feb 06, 2007 12:33 pm Post subject: Posted: Tue Feb 06, 2007 12:33 pm Post subject: |
 |
|
>How the hell can you go up to 239 of grid resolution?!?

265 is ok 
and export
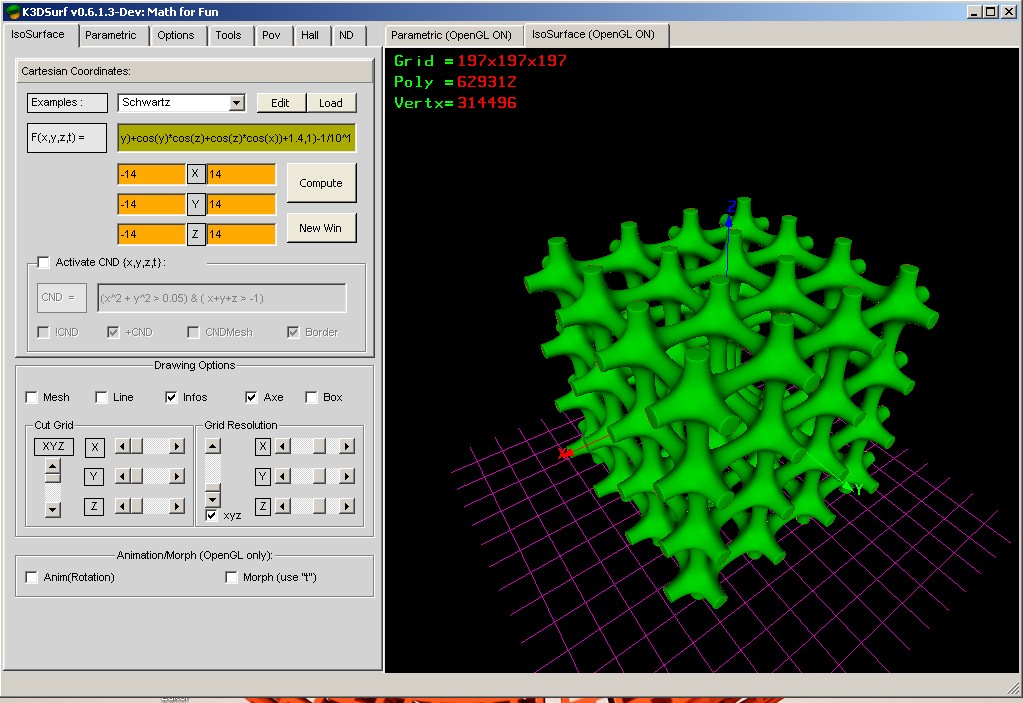
very nice 
-1/10^1
-1/10^0.1
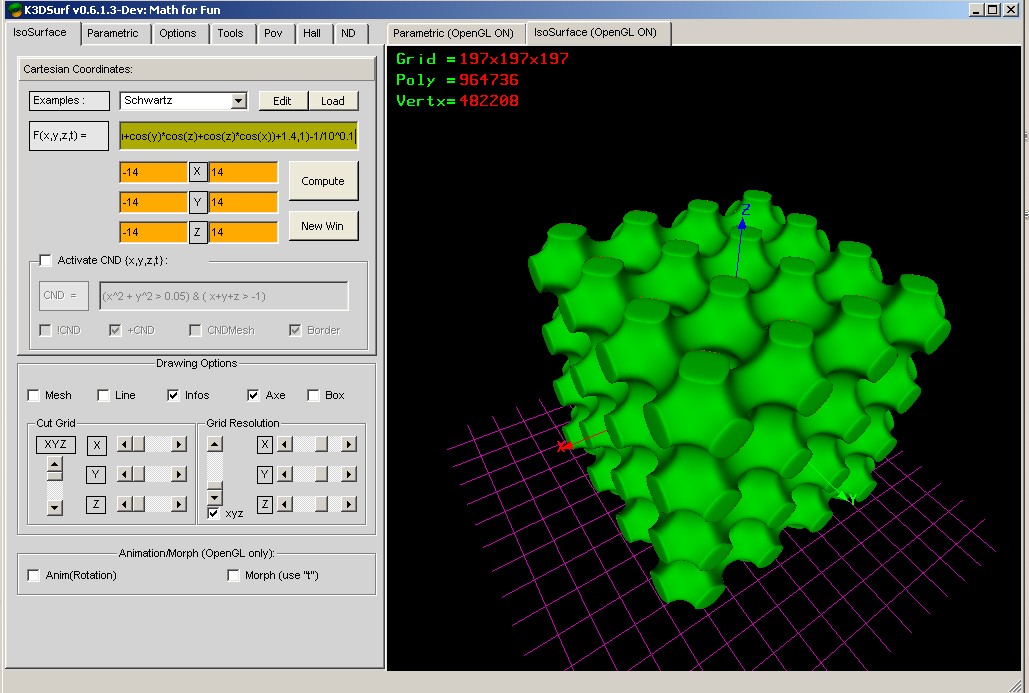
ciao
torofl
_________________
Kontakte |
|
| Back to top |
     |
 |
|