|
| View previous topic :: View next topic |
| Author |
Message |
nextstep
Site Admin
Joined: 06 Jan 2007
Posts: 539
|
 Posted: Tue Sep 11, 2007 7:53 am Post subject: Menger Sponge as an Isosurface? Posted: Tue Sep 11, 2007 7:53 am Post subject: Menger Sponge as an Isosurface? |
 |
|
Hi all,
This is an attempt to draw the Menger Sponge cube at a fourth level (M4) with K3DSurf  . .
This example shows that the resolution of this model should be correct with a grid >150 but the complete definition of this model (the Isosurface formula) should take some hundred of pages  . .
Maybe there is a better way to define it...It should be great to have a super compact formulas to draw it 
| Code: | Name: MengerSponge
F(): if((x^2 >0.109 | y^2>.109) &(z^2 >0.109 | y^2>.109) & (x^2 >0.109 | z^2>.109) &((x-2/3)^2 >0.0123456789 | (y-2/3)^2> 0.0123456789)&((x-2/3)^2 >0.0123456789 | (z-2/3)^2> 0.0123456789)&((y-2/3)^2 >0.0123456789 | (z-2/3)^2> 0.0123456789)&((x-2/3-2/9)^2 >0.0013717 | (y-2/3-2/9)^2> 0.0013717)&((x-2/3-2/9)^2 >0.0013717 | (z-2/3-2/9)^2> 0.0013717)&((y-2/3-2/9)^2 >0.0013717 | (z-2/3-2/9)^2>0.0013717 )&((x-2/3-2/9-2/27)^2 >.00015241383936 | (y-2/3-2/9-2/27)^2>.00015241383936 )&((x-2/3-2/9-2/27)^2 >.00015241383936 | (z-2/3-2/9-2/27)^2> .00015241383936)&((y-2/3-2/9-2/27)^2 >.00015241383936 | (z-2/3-2/9-2/27)^2>.00015241383936 ), x^100 + y^100 + z^100 -1, 1)
[x]: -1.01 , 1.01
[y]: -1.01 , 1.01
[z]: -1.01 , 1.01
; |
_________________
Cheers,
Abderrahman
Last edited by nextstep on Sat May 24, 2014 11:57 pm; edited 1 time in total |
|
| Back to top |
  |
 |
jotero
Joined: 27 Jan 2007
Posts: 153
Location: Germany Hannover
|
 Posted: Tue Sep 11, 2007 9:40 am Post subject: Posted: Tue Sep 11, 2007 9:40 am Post subject: |
 |
|
hello all 
WOW  very good idea taha very good idea taha 
the finished model looks however differently 
ciao
torolf
_________________
Kontakte |
|
| Back to top |
     |
 |
nextstep
Site Admin
Joined: 06 Jan 2007
Posts: 539
|
 Posted: Tue Sep 11, 2007 9:53 pm Post subject: Posted: Tue Sep 11, 2007 9:53 pm Post subject: |
 |
|
Hi all,
Thanks Torolf and here is the Menger Sponge at level 2 .
I think I've found a way to make it up to the level 4  . .
wait and see 
| Quote: | Name: MengerSponge_L2
F(): if(( abs(x) >1/3 | abs(y) > 1/3 ) &( abs(z) >1/3 | abs(y) > 1/3 ) &( abs(x) >1/3 | abs(z) > 1/3 ) & ( (( ( (abs(x-2/3) <1/9) + (abs(x+2/3) <1/9) + (abs(x) <1/9) ) * ((abs(y-2/3) < 1/9) +(abs(y) < 1/9) +(abs(y+2/3) <1/9) + (abs(z-2/3) < 1/9) +(abs(z) < 1/9) + (abs(z+2/3) < 1/9))) +( ( (abs(z-2/3) <1/9) + (abs(z+2/3) <1/9) + (abs(z) <1/9) ) * ( (abs(y-2/3) < 1/9) + (abs(y) < 1/9) + (abs(y+2/3) < 1/9))) ) =0), x^100 + y^100 + z^100 -1,1)
[x]: -1.001 , 1.001
[y]: -1.001 , 1.001
[z]: -1.001 , 1.001; |
_________________
Cheers,
Abderrahman
Last edited by nextstep on Sat May 24, 2014 11:57 pm; edited 1 time in total |
|
| Back to top |
  |
 |
nextstep
Site Admin
Joined: 06 Jan 2007
Posts: 539
|
 Posted: Wed Sep 12, 2007 4:03 am Post subject: Posted: Wed Sep 12, 2007 4:03 am Post subject: |
 |
|
Hi all,
Welcome to the Menger Sponge Level 3  : :
| Quote: | Name: MS3
F(): if(( abs(x) >1/3 | abs(y) > 1/3 ) &( abs(z) >1/3 | abs(y) > 1/3 ) &( abs(x) >1/3 | abs(z) > 1/3 ) & ( (( ( (abs(x-2/3) <1/9) + (abs(x+2/3) <1/9) + (abs(x) <1/9) ) * ((abs(y-2/3) < 1/9) +(abs(y) < 1/9) +(abs(y+2/3) <1/9) + (abs(z-2/3) < 1/9) +(abs(z) < 1/9) + (abs(z+2/3) < 1/9))) +( ( (abs(z-2/3) <1/9) + (abs(z+2/3) <1/9) + (abs(z) <1/9) ) * ( (abs(y-2/3) < 1/9) + (abs(y) < 1/9) + (abs(y+2/3) < 1/9))) ) =0)&( (( ( (abs(x-2/3) <1/27)+(abs(x-2/3-2/9) <1/27) + (abs(x-2/3+2/9) <1/27) +(abs(x+2/3) <1/27) +(abs(x+2/3-2/9) <1/27) + (abs(x+2/3+2/9) <1/27) +(abs(x) <1/27) + (abs(x-2/9) <1/27) + (abs(x+2/9) <1/27)) * ((abs(y-2/3) < 1/27) + (abs(y-2/3-2/9) < 1/27) + (abs(y-2/3+2/9) < 1/27) +(abs(y) < 1/27) + (abs(y-2/9) < 1/27) + (abs(y+2/9) < 1/27) + (abs(y+2/3) <1/27) + (abs(y+2/3-2/9) <1/27) + (abs(y+2/3+2/9) <1/27) + (abs(z-2/3) < 1/27) + (abs(z-2/3-2/9) < 1/27) + (abs(z-2/3+2/9) < 1/27) + (abs(z) < 1/27) + (abs(z-2/9) < 1/27) + (abs(z+2/9) < 1/27) + (abs(z+2/3) < 1/27) + (abs(z+2/3-2/9) < 1/27) + (abs(z+2/3+2/9) < 1/27) )) +( ( (abs(z-2/3) <1/27) + (abs(z-2/3-2/9) <1/27) + (abs(z-2/3+2/9) <1/27) + (abs(z+2/3) <1/27) + (abs(z+2/3-2/9) <1/27) + (abs(z+2/3+2/9) <1/27) + (abs(z) <1/27) + (abs(z-2/9) <1/27) + (abs(z+2/9) <1/27) ) * ( (abs(y-2/3) < 1/27) + (abs(y-2/3-2/9) < 1/27) + (abs(y-2/3+2/9) < 1/27) + (abs(y) < 1/27) + (abs(y-2/9) < 1/27) + (abs(y+2/9) < 1/27) + (abs(y+2/3) < 1/27) + (abs(y+2/3-2/9) < 1/27) + (abs(y+2/3+2/9) < 1/27)))) =0), x^100 + y^100 + z^100 -1,1)
[x]: -1.001 , 1.001
[y]: -1.001 , 1.001
[z]: -1.001 , 1.001
; |
Now, we still have only one level to reach the M4!

_________________
Cheers,
Abderrahman
Last edited by nextstep on Sat May 24, 2014 11:58 pm; edited 1 time in total |
|
| Back to top |
  |
 |
jotero
Joined: 27 Jan 2007
Posts: 153
Location: Germany Hannover
|
 Posted: Wed Sep 12, 2007 4:13 am Post subject: Posted: Wed Sep 12, 2007 4:13 am Post subject: |
 |
|
hello all 
i am speechless! very well made of you taha  
ciao
torolf
_________________
Kontakte |
|
| Back to top |
     |
 |
nextstep
Site Admin
Joined: 06 Jan 2007
Posts: 539
|
 Posted: Wed Sep 12, 2007 7:42 pm Post subject: Menger Sponge level 4 Posted: Wed Sep 12, 2007 7:42 pm Post subject: Menger Sponge level 4 |
 |
|
Hi all,
Thanks Torolf and here it is the famous Menger Sponge level 4 :  | Quote: | Name: MS4
F(): if(( abs(x) >1/3 | abs(y) > 1/3 ) &( abs(z) >1/3 | abs(y) > 1/3 ) &( abs(x) >1/3 | abs(z) > 1/3 )
&
( (( ( (abs(x-2/3) <1/9) + (abs(x+2/3) <1/9) + (abs(x) <1/9) ) * ((abs(y-2/3) < 1/9) +(abs(y) < 1/9) +(abs(y+2/3) <1/9) + (abs(z-2/3) < 1/9) +(abs(z) < 1/9) + (abs(z+2/3) < 1/9))) +( ( (abs(z-2/3) <1/9) + (abs(z+2/3) <1/9) + (abs(z) <1/9) ) * ( (abs(y-2/3) < 1/9) + (abs(y) < 1/9) + (abs(y+2/3) < 1/9))) ) =0)
&
( (( ( (abs(x-2/3) <1/27)+(abs(x-2/3-2/9) <1/27) + (abs(x-2/3+2/9) <1/27) +(abs(x+2/3) <1/27) +(abs(x+2/3-2/9) <1/27) + (abs(x+2/3+2/9) <1/27) +(abs(x) <1/27) + (abs(x-2/9) <1/27) + (abs(x+2/9) <1/27)) * ((abs(y-2/3) < 1/27) + (abs(y-2/3-2/9) < 1/27) + (abs(y-2/3+2/9) < 1/27) +(abs(y) < 1/27) + (abs(y-2/9) < 1/27) + (abs(y+2/9) < 1/27) + (abs(y+2/3) <1/27) + (abs(y+2/3-2/9) <1/27) + (abs(y+2/3+2/9) <1/27) + (abs(z-2/3) < 1/27) + (abs(z-2/3-2/9) < 1/27) + (abs(z-2/3+2/9) < 1/27) + (abs(z) < 1/27) + (abs(z-2/9) < 1/27) + (abs(z+2/9) < 1/27) + (abs(z+2/3) < 1/27) + (abs(z+2/3-2/9) < 1/27) + (abs(z+2/3+2/9) < 1/27) )) +( ( (abs(z-2/3) <1/27) + (abs(z-2/3-2/9) <1/27) + (abs(z-2/3+2/9) <1/27) + (abs(z+2/3) <1/27) + (abs(z+2/3-2/9) <1/27) + (abs(z+2/3+2/9) <1/27) + (abs(z) <1/27) + (abs(z-2/9) <1/27) + (abs(z+2/9) <1/27) ) * ( (abs(y-2/3) < 1/27) + (abs(y-2/3-2/9) < 1/27) + (abs(y-2/3+2/9) < 1/27) + (abs(y) < 1/27) + (abs(y-2/9) < 1/27) + (abs(y+2/9) < 1/27) + (abs(y+2/3) < 1/27) + (abs(y+2/3-2/9) < 1/27) + (abs(y+2/3+2/9) < 1/27)))) =0)
&
( ((
(
(abs(x-2/3) <1/81)+ (abs(x-2/3-2/27) <1/81)+ (abs(x-2/3+2/27) <1/81)+
(abs(x-2/3-2/9) <1/81) + (abs(x-2/3-2/9-2/27) <1/81) + (abs(x-2/3-2/9+2/27) <1/81) +
(abs(x-2/3+2/9) <1/81) +(abs(x-2/3+2/9-2/27) <1/81) +(abs(x-2/3+2/9+2/27) <1/81) +
(abs(x+2/3) <1/81) +(abs(x+2/3-2/27) <1/81) +(abs(x+2/3+2/27) <1/81) +
(abs(x+2/3-2/9) <1/81) +(abs(x+2/3-2/9-2/27) <1/81) +(abs(x+2/3-2/9+2/27) <1/81) +
(abs(x+2/3+2/9) <1/81) +(abs(x+2/3+2/9-2/27) <1/81) +(abs(x+2/3+2/9+2/27) <1/81) +
(abs(x) <1/81) + (abs(x-2/27) <1/81) +(abs(x+2/27) <1/81) +
(abs(x-2/9) <1/81) + (abs(x-2/9-2/27) <1/81) + (abs(x-2/9+2/27) <1/81) +
(abs(x+2/9) <1/81)+(abs(x+2/9-2/27) <1/81)+(abs(x+2/9+2/27) <1/81)
) *
(
(abs(y-2/3) < 1/81) + (abs(y-2/3-2/27) < 1/81) +(abs(y-2/3+2/27) < 1/81) +
(abs(y-2/3-2/9) < 1/81) + (abs(y-2/3-2/9-2/27) < 1/81) +(abs(y-2/3-2/9+2/27) < 1/81) +
(abs(y-2/3+2/9) < 1/81) +(abs(y-2/3+2/9-2/27) < 1/81) +(abs(y-2/3+2/9+2/27) < 1/81) +
(abs(y) < 1/81) + (abs(y-2/27) < 1/81) + (abs(y+2/27) < 1/81) +
(abs(y-2/9) < 1/81) + (abs(y-2/9-2/27) < 1/81) + (abs(y-2/9+2/27) < 1/81) +
(abs(y+2/9) < 1/81) + (abs(y+2/9-2/27) < 1/81) + (abs(y+2/9+2/27) < 1/81) +
(abs(y+2/3) <1/81) + (abs(y+2/3-2/27) <1/81) + (abs(y+2/3+2/27) <1/81) +
(abs(y+2/3-2/9) <1/81) + (abs(y+2/3-2/9-2/27) <1/81) + (abs(y+2/3-2/9+2/27) <1/81) +
(abs(y+2/3+2/9) <1/81) + (abs(y+2/3+2/9-2/27) <1/81) + (abs(y+2/3+2/9+2/27) <1/81) +
(abs(z-2/3) < 1/81) + (abs(z-2/3-2/27) < 1/81) + (abs(z-2/3+2/27) < 1/81) +
(abs(z-2/3-2/9) < 1/81) + (abs(z-2/3-2/9-2/27) < 1/81) + (abs(z-2/3-2/9+2/27) < 1/81) +
(abs(z-2/3+2/9) < 1/81) + (abs(z-2/3+2/9-2/27) < 1/81) + (abs(z-2/3+2/9+2/27) < 1/81) +
(abs(z) < 1/81) + (abs(z-2/27) < 1/81) + (abs(z+2/27) < 1/81) +
(abs(z-2/9) < 1/81) + (abs(z-2/9-2/27) < 1/81) + (abs(z-2/9+2/27) < 1/81) +
(abs(z+2/9) < 1/81) + (abs(z+2/9-2/27) < 1/81) + (abs(z+2/9+2/27) < 1/81) +
(abs(z+2/3) < 1/81) + (abs(z+2/3-2/27) < 1/81) + (abs(z+2/3+2/27) < 1/81) +
(abs(z+2/3-2/9) < 1/81) + (abs(z+2/3-2/9-2/27) < 1/81) + (abs(z+2/3-2/9+2/27) < 1/81) +
(abs(z+2/3+2/9) < 1/81) +(abs(z+2/3+2/9-2/27) < 1/81) +(abs(z+2/3+2/9+2/27) < 1/81)
)) +
(
(
(abs(z-2/3) <1/81) + (abs(z-2/3-2/27) <1/81) + (abs(z-2/3+2/27) <1/81) +
(abs(z-2/3-2/9) <1/81) + (abs(z-2/3-2/9-2/27) <1/81) + (abs(z-2/3-2/9+2/27) <1/81) +
(abs(z-2/3+2/9) <1/81) + (abs(z-2/3+2/9-2/27) <1/81) + (abs(z-2/3+2/9+2/27) <1/81) +
(abs(z+2/3) <1/81) + (abs(z+2/3-2/27) <1/81) + (abs(z+2/3+2/27) <1/81) +
(abs(z+2/3-2/9) <1/81) + (abs(z+2/3-2/9-2/27) <1/81) + (abs(z+2/3-2/9+2/27) <1/81) +
(abs(z+2/3+2/9) <1/81) + (abs(z+2/3+2/9-2/27) <1/81) + (abs(z+2/3+2/9+2/27) <1/81) +
(abs(z) <1/81) + (abs(z-2/27) <1/81) + (abs(z+2/27) <1/81) +
(abs(z-2/9) <1/81) + (abs(z-2/9-2/27) <1/81) + (abs(z-2/9+2/27) <1/81) +
(abs(z+2/9) <1/81) + (abs(z+2/9-2/27) <1/81) + (abs(z+2/9+2/27) <1/81)
) * (
(abs(y-2/3) < 1/81) + (abs(y-2/3-2/27) < 1/81) + (abs(y-2/3+2/27) < 1/81) +
(abs(y-2/3-2/9) < 1/81) + (abs(y-2/3-2/9-2/27) < 1/81) + (abs(y-2/3-2/9+2/27) < 1/81) +
(abs(y-2/3+2/9) < 1/81) + (abs(y-2/3+2/9-2/27) < 1/81) + (abs(y-2/3+2/9+2/27) < 1/81) +
(abs(y) < 1/81) + (abs(y-2/27) < 1/81) + (abs(y+2/27) < 1/81) +
(abs(y-2/9) < 1/81) + (abs(y-2/9-2/27) < 1/81) + (abs(y-2/9+2/27) < 1/81) +
(abs(y+2/9) < 1/81) + (abs(y+2/9-2/27) < 1/81) + (abs(y+2/9+2/27) < 1/81) +
(abs(y+2/3) < 1/81) + (abs(y+2/3-2/27) < 1/81) + (abs(y+2/3+2/27) < 1/81) +
(abs(y+2/3-2/9) < 1/81) + (abs(y+2/3-2/9-2/27) < 1/81) + (abs(y+2/3-2/9+2/27) < 1/81) +
(abs(y+2/3+2/9) < 1/81) + (abs(y+2/3+2/9-2/27) < 1/81) + (abs(y+2/3+2/9+2/27) < 1/81)
)
)) =0)
, x^1000 + y^1000 + z^1000 -1,1)
[x]: -1.001 , 1.001
[y]: -1.001 , 1.001
[z]: -1.001 , 1.001
; |
Here you can see a detailed view ( 1/512) of the entire cube. This shows that this isosurface formulas is very accurate! I'll show later an algorithm for generating formulas for any level of the Menger Sponge. This maybe not the best description of the Menger Sponge but it has the advantage to be quite easy to write. Also, this opens new perspectives for new mathematical models!
Enjoy,
Taha

_________________
Cheers,
Abderrahman
Last edited by nextstep on Sat May 24, 2014 11:58 pm; edited 1 time in total |
|
| Back to top |
  |
 |
nextstep
Site Admin
Joined: 06 Jan 2007
Posts: 539
|
 Posted: Thu Sep 13, 2007 5:47 pm Post subject: Posted: Thu Sep 13, 2007 5:47 pm Post subject: |
 |
|
Hi all,
A new version of the Menger Sponge level 4. It's more than two times faster the previous one 
| Quote: |
Name: MengerSpongeL4_v2
F(): if(( abs(x) >1/3 | abs(y) > 1/3 ) &( abs(z) >1/3 | abs(y) > 1/3 ) &( abs(x) >1/3 | abs(z) > 1/3 ) ,
if(
( (( ( (abs(x-2/3) <1/9) + (abs(x+2/3) <1/9) + (abs(x) <1/9) ) * ((abs(y-2/3) < 1/9) +(abs(y) < 1/9) +(abs(y+2/3) <1/9) + (abs(z-2/3) < 1/9) +(abs(z) < 1/9) + (abs(z+2/3) < 1/9))) +( ( (abs(z-2/3) <1/9) + (abs(z+2/3) <1/9) + (abs(z) <1/9) ) * ( (abs(y-2/3) < 1/9) + (abs(y) < 1/9) + (abs(y+2/3) < 1/9))) ) =0),
if(
( (( ( (abs(x-2/3) <1/27)+(abs(x-2/3-2/9) <1/27) + (abs(x-2/3+2/9) <1/27) +(abs(x+2/3) <1/27) +(abs(x+2/3-2/9) <1/27) + (abs(x+2/3+2/9) <1/27) +(abs(x) <1/27) + (abs(x-2/9) <1/27) + (abs(x+2/9) <1/27)) * ((abs(y-2/3) < 1/27) + (abs(y-2/3-2/9) < 1/27) + (abs(y-2/3+2/9) < 1/27) +(abs(y) < 1/27) + (abs(y-2/9) < 1/27) + (abs(y+2/9) < 1/27) + (abs(y+2/3) <1/27) + (abs(y+2/3-2/9) <1/27) + (abs(y+2/3+2/9) <1/27) + (abs(z-2/3) < 1/27) + (abs(z-2/3-2/9) < 1/27) + (abs(z-2/3+2/9) < 1/27) + (abs(z) < 1/27) + (abs(z-2/9) < 1/27) + (abs(z+2/9) < 1/27) + (abs(z+2/3) < 1/27) + (abs(z+2/3-2/9) < 1/27) + (abs(z+2/3+2/9) < 1/27) )) +( ( (abs(z-2/3) <1/27) + (abs(z-2/3-2/9) <1/27) + (abs(z-2/3+2/9) <1/27) + (abs(z+2/3) <1/27) + (abs(z+2/3-2/9) <1/27) + (abs(z+2/3+2/9) <1/27) + (abs(z) <1/27) + (abs(z-2/9) <1/27) + (abs(z+2/9) <1/27) ) * ( (abs(y-2/3) < 1/27) + (abs(y-2/3-2/9) < 1/27) + (abs(y-2/3+2/9) < 1/27) + (abs(y) < 1/27) + (abs(y-2/9) < 1/27) + (abs(y+2/9) < 1/27) + (abs(y+2/3) < 1/27) + (abs(y+2/3-2/9) < 1/27) + (abs(y+2/3+2/9) < 1/27)))) =0),
if(
( ((
(
(abs(x-2/3) <1/81)+ (abs(x-2/3-2/27) <1/81)+ (abs(x-2/3+2/27) <1/81)+
(abs(x-2/3-2/9) <1/81) + (abs(x-2/3-2/9-2/27) <1/81) + (abs(x-2/3-2/9+2/27) <1/81) +
(abs(x-2/3+2/9) <1/81) +(abs(x-2/3+2/9-2/27) <1/81) +(abs(x-2/3+2/9+2/27) <1/81) +
(abs(x+2/3) <1/81) +(abs(x+2/3-2/27) <1/81) +(abs(x+2/3+2/27) <1/81) +
(abs(x+2/3-2/9) <1/81) +(abs(x+2/3-2/9-2/27) <1/81) +(abs(x+2/3-2/9+2/27) <1/81) +
(abs(x+2/3+2/9) <1/81) +(abs(x+2/3+2/9-2/27) <1/81) +(abs(x+2/3+2/9+2/27) <1/81) +
(abs(x) <1/81) + (abs(x-2/27) <1/81) +(abs(x+2/27) <1/81) +
(abs(x-2/9) <1/81) + (abs(x-2/9-2/27) <1/81) + (abs(x-2/9+2/27) <1/81) +
(abs(x+2/9) <1/81)+(abs(x+2/9-2/27) <1/81)+(abs(x+2/9+2/27) <1/81)
) *
(
(abs(y-2/3) < 1/81) + (abs(y-2/3-2/27) < 1/81) +(abs(y-2/3+2/27) < 1/81) +
(abs(y-2/3-2/9) < 1/81) + (abs(y-2/3-2/9-2/27) < 1/81) +(abs(y-2/3-2/9+2/27) < 1/81) +
(abs(y-2/3+2/9) < 1/81) +(abs(y-2/3+2/9-2/27) < 1/81) +(abs(y-2/3+2/9+2/27) < 1/81) +
(abs(y) < 1/81) + (abs(y-2/27) < 1/81) + (abs(y+2/27) < 1/81) +
(abs(y-2/9) < 1/81) + (abs(y-2/9-2/27) < 1/81) + (abs(y-2/9+2/27) < 1/81) +
(abs(y+2/9) < 1/81) + (abs(y+2/9-2/27) < 1/81) + (abs(y+2/9+2/27) < 1/81) +
(abs(y+2/3) <1/81) + (abs(y+2/3-2/27) <1/81) + (abs(y+2/3+2/27) <1/81) +
(abs(y+2/3-2/9) <1/81) + (abs(y+2/3-2/9-2/27) <1/81) + (abs(y+2/3-2/9+2/27) <1/81) +
(abs(y+2/3+2/9) <1/81) + (abs(y+2/3+2/9-2/27) <1/81) + (abs(y+2/3+2/9+2/27) <1/81) +
(abs(z-2/3) < 1/81) + (abs(z-2/3-2/27) < 1/81) + (abs(z-2/3+2/27) < 1/81) +
(abs(z-2/3-2/9) < 1/81) + (abs(z-2/3-2/9-2/27) < 1/81) + (abs(z-2/3-2/9+2/27) < 1/81) +
(abs(z-2/3+2/9) < 1/81) + (abs(z-2/3+2/9-2/27) < 1/81) + (abs(z-2/3+2/9+2/27) < 1/81) +
(abs(z) < 1/81) + (abs(z-2/27) < 1/81) + (abs(z+2/27) < 1/81) +
(abs(z-2/9) < 1/81) + (abs(z-2/9-2/27) < 1/81) + (abs(z-2/9+2/27) < 1/81) +
(abs(z+2/9) < 1/81) + (abs(z+2/9-2/27) < 1/81) + (abs(z+2/9+2/27) < 1/81) +
(abs(z+2/3) < 1/81) + (abs(z+2/3-2/27) < 1/81) + (abs(z+2/3+2/27) < 1/81) +
(abs(z+2/3-2/9) < 1/81) + (abs(z+2/3-2/9-2/27) < 1/81) + (abs(z+2/3-2/9+2/27) < 1/81) +
(abs(z+2/3+2/9) < 1/81) +(abs(z+2/3+2/9-2/27) < 1/81) +(abs(z+2/3+2/9+2/27) < 1/81)
)) +
(
(
(abs(z-2/3) <1/81) + (abs(z-2/3-2/27) <1/81) + (abs(z-2/3+2/27) <1/81) +
(abs(z-2/3-2/9) <1/81) + (abs(z-2/3-2/9-2/27) <1/81) + (abs(z-2/3-2/9+2/27) <1/81) +
(abs(z-2/3+2/9) <1/81) + (abs(z-2/3+2/9-2/27) <1/81) + (abs(z-2/3+2/9+2/27) <1/81) +
(abs(z+2/3) <1/81) + (abs(z+2/3-2/27) <1/81) + (abs(z+2/3+2/27) <1/81) +
(abs(z+2/3-2/9) <1/81) + (abs(z+2/3-2/9-2/27) <1/81) + (abs(z+2/3-2/9+2/27) <1/81) +
(abs(z+2/3+2/9) <1/81) + (abs(z+2/3+2/9-2/27) <1/81) + (abs(z+2/3+2/9+2/27) <1/81) +
(abs(z) <1/81) + (abs(z-2/27) <1/81) + (abs(z+2/27) <1/81) +
(abs(z-2/9) <1/81) + (abs(z-2/9-2/27) <1/81) + (abs(z-2/9+2/27) <1/81) +
(abs(z+2/9) <1/81) + (abs(z+2/9-2/27) <1/81) + (abs(z+2/9+2/27) <1/81)
) * (
(abs(y-2/3) < 1/81) + (abs(y-2/3-2/27) < 1/81) + (abs(y-2/3+2/27) < 1/81) +
(abs(y-2/3-2/9) < 1/81) + (abs(y-2/3-2/9-2/27) < 1/81) + (abs(y-2/3-2/9+2/27) < 1/81) +
(abs(y-2/3+2/9) < 1/81) + (abs(y-2/3+2/9-2/27) < 1/81) + (abs(y-2/3+2/9+2/27) < 1/81) +
(abs(y) < 1/81) + (abs(y-2/27) < 1/81) + (abs(y+2/27) < 1/81) +
(abs(y-2/9) < 1/81) + (abs(y-2/9-2/27) < 1/81) + (abs(y-2/9+2/27) < 1/81) +
(abs(y+2/9) < 1/81) + (abs(y+2/9-2/27) < 1/81) + (abs(y+2/9+2/27) < 1/81) +
(abs(y+2/3) < 1/81) + (abs(y+2/3-2/27) < 1/81) + (abs(y+2/3+2/27) < 1/81) +
(abs(y+2/3-2/9) < 1/81) + (abs(y+2/3-2/9-2/27) < 1/81) + (abs(y+2/3-2/9+2/27) < 1/81) +
(abs(y+2/3+2/9) < 1/81) + (abs(y+2/3+2/9-2/27) < 1/81) + (abs(y+2/3+2/9+2/27) < 1/81)
)
)) =0)
, x^1000 + y^1000 + z^1000 -1, 1), 1), 1), 1)
[x]: -1.001 , 1.001
[y]: -1.001 , 1.001
[z]: -1.001 , 1.001
;
|
_________________
Cheers,
Abderrahman |
|
| Back to top |
  |
 |
inode

Joined: 27 Jan 2007
Posts: 127
Location: Austria
|
 Posted: Fri Sep 14, 2007 11:28 pm Post subject: Posted: Fri Sep 14, 2007 11:28 pm Post subject: |
 |
|
MengerSponge + Pacman = MengerPacman ( ) )
| Quote: | Name: MengerPacman
F(): if((abs(x)>t/2 | abs(y)>t/2)
&(abs(z)>t/2 | abs(y)>t/2)
&(abs(x)>t/2 | abs(z)>t/2)
& (((((abs(x-2/3)<t/6) + (abs(x+2/3)<t/6) + (abs(x)<t/6))
* ((abs(y-2/3)<t/6) + (abs(y)<t/6) + (abs(y+2/3)<t/6)
+ (abs(z-2/3)<t/6) + (abs(z)<t/6) + (abs(z+2/3)<t/6)))
+ (((abs(z-2/3)<t/6) + (abs(z+2/3)<t/6) + (abs(z)<t/6))
* ((abs(y-2/3)<t/6) + (abs(y)<t/6) + (abs(y+2/3)<t/6)))) =0)
, x^100 + y^100 + z^100 -1,1)
[x]: -1.001 , 1.001
[y]: -1.001 , 1.001
[z]: -1.001 , 1.001
; |
set grid to 32x32x32 and start morphing  Gerd Gerd
ps. for me Menger Sponge L4 looks like a brain twister.
that can't be created by hand - or?
pps. formula definition would be clearer and easier to define using constants
(e.g. k1=1/3; k2=1/9; k3=2/3-2/27; etc...)
do you think calculation would be also faster with constant definitions? |
|
| Back to top |
  |
 |
nextstep
Site Admin
Joined: 06 Jan 2007
Posts: 539
|
 Posted: Sun Sep 16, 2007 6:08 am Post subject: Posted: Sun Sep 16, 2007 6:08 am Post subject: |
 |
|
Hi all,
The MengerPacman variation is very interesting. Thanks 
| Quote: | ps. for me Menger Sponge L4 looks like a brain twister.
that can't be created by hand - or? |
It's a brain twister however it can be made by hand and the proof is on the top  . This shows that there are plenty of discoveries to be made by using isosurfaces. . This shows that there are plenty of discoveries to be made by using isosurfaces.
| Quote: |
pps. formula definition would be clearer and easier to define using constants
(e.g. k1=1/3; k2=1/9; k3=2/3-2/27; etc...) |
Of course however this can hide some details to me in the process of optimization, so right now I prefer to let things as they are...
| Quote: |
do you think calculation would be also faster with constant definitions? |
Yes and calculations will be much more faster with an optimization of the formulas itself (compare the two versions of the MS4 and I'm still working on the third versions  ). ).
_________________
Cheers,
Abderrahman |
|
| Back to top |
  |
 |
nextstep
Site Admin
Joined: 06 Jan 2007
Posts: 539
|
 Posted: Fri Sep 21, 2007 5:58 am Post subject: Posted: Fri Sep 21, 2007 5:58 am Post subject: |
 |
|
Hi all,
| Quote: |
do you think calculation would be also faster with constant definitions? |
K3DSurf 0.6.2 has an unique feature that make it extremely fast: I really think it's the fastest mathematical tool ever made (including the commercial ones like Mathematica)  . Why I'm saying that? because it includes a new mathematical parser technology for height speed calculations. As far as I know, there is no references to this on the specialized books or in the literature. So, lets play with it to see what can we get from this "secret" tool . Why I'm saying that? because it includes a new mathematical parser technology for height speed calculations. As far as I know, there is no references to this on the specialized books or in the literature. So, lets play with it to see what can we get from this "secret" tool  . .
First, this tool support all mathematical functions...except the "if" instruction  so we have to eliminate it from the MS4 formulas. so we have to eliminate it from the MS4 formulas.
The first Menger Sponge level 4 isosurface can be changed to this (to eliminate the "if" instruction).
| Quote: | Name: MS4
F(): -( x^100 + y^100 + z^100 -1)*
((abs(x) >1/3 | abs(y) > 1/3)*(abs(x) >1/3 | abs(z) > 1/3)*(abs(z) >1/3 | abs(y) > 1/3))
* ( (((abs(x-2/3) <1/9) + (abs(x+2/3) <1/9) + (abs(x) <1/9))*((abs(y-2/3) <1/9) + (abs(y+2/3) <1/9) + (abs(y) <1/9)+(abs(z-2/3) <1/9) + (abs(z+2/3) <1/9) + (abs(z) <1/9)) + ((abs(z-2/3) <1/9) + (abs(z+2/3) <1/9) + (abs(z) <1/9))*((abs(y-2/3) <1/9) + (abs(y+2/3) <1/9) + (abs(y) <1/9))) =0)
* ( (((abs(x-2/3) <1/27)+(abs(x-2/3-2/9) <1/27) + (abs(x-2/3+2/9) <1/27) +(abs(x+2/3) <1/27) +(abs(x+2/3-2/9) <1/27) + (abs(x+2/3+2/9) <1/27) +(abs(x) <1/27) + (abs(x-2/9) <1/27) + (abs(x+2/9) <1/27))*((abs(y-2/3) <1/27)+(abs(y-2/3-2/9) <1/27) + (abs(y-2/3+2/9) <1/27) +(abs(y+2/3) <1/27) +(abs(y+2/3-2/9) <1/27) + (abs(y+2/3+2/9) <1/27) +(abs(y) <1/27) + (abs(y-2/9) <1/27) + (abs(y+2/9) <1/27)+(abs(z-2/3) <1/27)+(abs(z-2/3-2/9) <1/27) + (abs(z-2/3+2/9) <1/27) +(abs(z+2/3) <1/27) +(abs(z+2/3-2/9) <1/27) + (abs(z+2/3+2/9) <1/27) +(abs(z) <1/27) + (abs(z-2/9) <1/27) + (abs(z+2/9) <1/27)) + ((abs(z-2/3) <1/27)+(abs(z-2/3-2/9) <1/27) + (abs(z-2/3+2/9) <1/27) +(abs(z+2/3) <1/27) +(abs(z+2/3-2/9) <1/27) + (abs(z+2/3+2/9) <1/27) +(abs(z) <1/27) + (abs(z-2/9) <1/27) + (abs(z+2/9) <1/27))*((abs(y-2/3) <1/27)+(abs(y-2/3-2/9) <1/27) + (abs(y-2/3+2/9) <1/27) +(abs(y+2/3) <1/27) +(abs(y+2/3-2/9) <1/27) + (abs(y+2/3+2/9) <1/27) +(abs(y) <1/27) + (abs(y-2/9) <1/27) + (abs(y+2/9) <1/27))) =0)
* ( ( ((abs(x-2/3) <1/81)+ (abs(x-2/3-2/27) <1/81)+ (abs(x-2/3+2/27) <1/81)+
(abs(x-2/3-2/9) <1/81) + (abs(x-2/3-2/9-2/27) <1/81) + (abs(x-2/3-2/9+2/27) <1/81) +
(abs(x-2/3+2/9) <1/81) +(abs(x-2/3+2/9-2/27) <1/81) +(abs(x-2/3+2/9+2/27) <1/81) +
(abs(x+2/3) <1/81) +(abs(x+2/3-2/27) <1/81) +(abs(x+2/3+2/27) <1/81) +
(abs(x+2/3-2/9) <1/81) +(abs(x+2/3-2/9-2/27) <1/81) +(abs(x+2/3-2/9+2/27) <1/81) +
(abs(x+2/3+2/9) <1/81) +(abs(x+2/3+2/9-2/27) <1/81) +(abs(x+2/3+2/9+2/27) <1/81) +
(abs(x) <1/81) + (abs(x-2/27) <1/81) +(abs(x+2/27) <1/81) +
(abs(x-2/9) <1/81) + (abs(x-2/9-2/27) <1/81) + (abs(x-2/9+2/27) <1/81) +
(abs(x+2/9) <1/81)+(abs(x+2/9-2/27) <1/81)+(abs(x+2/9+2/27) <1/81)
) *(((abs(y-2/3) <1/81)+ (abs(y-2/3-2/27) <1/81)+ (abs(y-2/3+2/27) <1/81)+
(abs(y-2/3-2/9) <1/81) + (abs(y-2/3-2/9-2/27) <1/81) + (abs(y-2/3-2/9+2/27) <1/81) +
(abs(y-2/3+2/9) <1/81) +(abs(y-2/3+2/9-2/27) <1/81) +(abs(y-2/3+2/9+2/27) <1/81) +
(abs(y+2/3) <1/81) +(abs(y+2/3-2/27) <1/81) +(abs(y+2/3+2/27) <1/81) +
(abs(y+2/3-2/9) <1/81) +(abs(y+2/3-2/9-2/27) <1/81) +(abs(y+2/3-2/9+2/27) <1/81) +
(abs(y+2/3+2/9) <1/81) +(abs(y+2/3+2/9-2/27) <1/81) +(abs(y+2/3+2/9+2/27) <1/81) +
(abs(y) <1/81) + (abs(y-2/27) <1/81) +(abs(y+2/27) <1/81) +
(abs(y-2/9) <1/81) + (abs(y-2/9-2/27) <1/81) + (abs(y-2/9+2/27) <1/81) +
(abs(y+2/9) <1/81)+(abs(y+2/9-2/27) <1/81)+(abs(y+2/9+2/27) <1/81)
)+((abs(z-2/3) <1/81)+ (abs(z-2/3-2/27) <1/81)+ (abs(z-2/3+2/27) <1/81)+
(abs(z-2/3-2/9) <1/81) + (abs(z-2/3-2/9-2/27) <1/81) + (abs(z-2/3-2/9+2/27) <1/81) +
(abs(z-2/3+2/9) <1/81) +(abs(z-2/3+2/9-2/27) <1/81) +(abs(z-2/3+2/9+2/27) <1/81) +
(abs(z+2/3) <1/81) +(abs(z+2/3-2/27) <1/81) +(abs(z+2/3+2/27) <1/81) +
(abs(z+2/3-2/9) <1/81) +(abs(z+2/3-2/9-2/27) <1/81) +(abs(z+2/3-2/9+2/27) <1/81) +
(abs(z+2/3+2/9) <1/81) +(abs(z+2/3+2/9-2/27) <1/81) +(abs(z+2/3+2/9+2/27) <1/81) +
(abs(z) <1/81) + (abs(z-2/27) <1/81) +(abs(z+2/27) <1/81) +
(abs(z-2/9) <1/81) + (abs(z-2/9-2/27) <1/81) + (abs(z-2/9+2/27) <1/81) +
(abs(z+2/9) <1/81)+(abs(z+2/9-2/27) <1/81)+(abs(z+2/9+2/27) <1/81))) + ((abs(z-2/3) <1/81)+ (abs(z-2/3-2/27) <1/81)+ (abs(z-2/3+2/27) <1/81)+
(abs(z-2/3-2/9) <1/81) + (abs(z-2/3-2/9-2/27) <1/81) + (abs(z-2/3-2/9+2/27) <1/81) +
(abs(z-2/3+2/9) <1/81) +(abs(z-2/3+2/9-2/27) <1/81) +(abs(z-2/3+2/9+2/27) <1/81) +
(abs(z+2/3) <1/81) +(abs(z+2/3-2/27) <1/81) +(abs(z+2/3+2/27) <1/81) +
(abs(z+2/3-2/9) <1/81) +(abs(z+2/3-2/9-2/27) <1/81) +(abs(z+2/3-2/9+2/27) <1/81) +
(abs(z+2/3+2/9) <1/81) +(abs(z+2/3+2/9-2/27) <1/81) +(abs(z+2/3+2/9+2/27) <1/81) +
(abs(z) <1/81) + (abs(z-2/27) <1/81) +(abs(z+2/27) <1/81) +
(abs(z-2/9) <1/81) + (abs(z-2/9-2/27) <1/81) + (abs(z-2/9+2/27) <1/81) +
(abs(z+2/9) <1/81)+(abs(z+2/9-2/27) <1/81)+(abs(z+2/9+2/27) <1/81))*((abs(y-2/3) <1/81)+ (abs(y-2/3-2/27) <1/81)+ (abs(y-2/3+2/27) <1/81)+
(abs(y-2/3-2/9) <1/81) + (abs(y-2/3-2/9-2/27) <1/81) + (abs(y-2/3-2/9+2/27) <1/81) +
(abs(y-2/3+2/9) <1/81) +(abs(y-2/3+2/9-2/27) <1/81) +(abs(y-2/3+2/9+2/27) <1/81) +
(abs(y+2/3) <1/81) +(abs(y+2/3-2/27) <1/81) +(abs(y+2/3+2/27) <1/81) +
(abs(y+2/3-2/9) <1/81) +(abs(y+2/3-2/9-2/27) <1/81) +(abs(y+2/3-2/9+2/27) <1/81) +
(abs(y+2/3+2/9) <1/81) +(abs(y+2/3+2/9-2/27) <1/81) +(abs(y+2/3+2/9+2/27) <1/81) +
(abs(y) <1/81) + (abs(y-2/27) <1/81) +(abs(y+2/27) <1/81) +
(abs(y-2/9) <1/81) + (abs(y-2/9-2/27) <1/81) + (abs(y-2/9+2/27) <1/81) +
(abs(y+2/9) <1/81)+(abs(y+2/9-2/27) <1/81)+(abs(y+2/9+2/27) <1/81))) =0)
[x]: -1.001 , 1.001
[y]: -1.001 , 1.001
[z]: -1.001 , 1.001
; |
Make some tests with this formula with height grid (example: 100)
Now activate this button like in this image and recalculate. As you can see, calculations are from 2 to 3 times faster just by activating this button!
The best part however is that we can boost the speed to even greater record...
The MS4 formula on the top is equivalent to this :
| Quote: | Name: MS4
F(): -( x^100 + y^100 + z^100 -1)*((Dxy * Dzy * Dxz) * ( (Cx*(Cy+Cz) + Cz*Cy) =0)*( (Bx*(By+Bz) + Bz*By) =0)*( (Ax*(Ay+Az) + Az*Ay) =0) )
[x]: -1.001 , 1.001
[y]: -1.001 , 1.001
[z]: -1.001 , 1.001
; |
Now, go to the same page and fill the four fields Au, Bu, Cu and D{u,v} as shown in the image with theses values :
| Quote: | A[u]: (abs(u-2/3) <1/81)+ (abs(u-2/3-2/27) <1/81)+ (abs(u-2/3+2/27) <1/81)+
(abs(u-2/3-2/9) <1/81) + (abs(u-2/3-2/9-2/27) <1/81) + (abs(u-2/3-2/9+2/27) <1/81) +
(abs(u-2/3+2/9) <1/81) +(abs(u-2/3+2/9-2/27) <1/81) +(abs(u-2/3+2/9+2/27) <1/81) +
(abs(u+2/3) <1/81) +(abs(u+2/3-2/27) <1/81) +(abs(u+2/3+2/27) <1/81) +
(abs(u+2/3-2/9) <1/81) +(abs(u+2/3-2/9-2/27) <1/81) +(abs(u+2/3-2/9+2/27) <1/81) +
(abs(u+2/3+2/9) <1/81) +(abs(u+2/3+2/9-2/27) <1/81) +(abs(u+2/3+2/9+2/27) <1/81) +
(abs(u) <1/81) + (abs(u-2/27) <1/81) +(abs(u+2/27) <1/81) +
(abs(u-2/9) <1/81) + (abs(u-2/9-2/27) <1/81) + (abs(u-2/9+2/27) <1/81) +
(abs(u+2/9) <1/81)+(abs(u+2/9-2/27) <1/81)+(abs(u+2/9+2/27) <1/81)
B[u]: (abs(u-2/3) <1/27)+(abs(u-2/3-2/9) <1/27) + (abs(u-2/3+2/9) <1/27) +(abs(u+2/3) <1/27) +(abs(u+2/3-2/9) <1/27) + (abs(u+2/3+2/9) <1/27) +(abs(u) <1/27) + (abs(u-2/9) <1/27) + (abs(u+2/9) <1/27)
C[u]: (abs(u-2/3) <1/9) + (abs(u+2/3) <1/9) + (abs(u) <1/9)
D[u,v]: abs(u) >1/3 | abs(v) > 1/3 |
Now, recalculate and enjoy the speed: You can be sure no one in the world had make the Menger Sponge Level 4 that fast (except me  ) )
In my case, it's more than 20 times faster .
Some precisions:
1) The grid value should be a multiple of 4 (ie, 4, 8, 12...)
2) There is other ways to make it even faster with this great K3DSurf tool ... 
_________________
Cheers,
Abderrahman
Last edited by nextstep on Sat May 24, 2014 11:59 pm; edited 1 time in total |
|
| Back to top |
  |
 |
nextstep
Site Admin
Joined: 06 Jan 2007
Posts: 539
|
 Posted: Mon May 19, 2014 12:35 am Post subject: Posted: Mon May 19, 2014 12:35 am Post subject: |
 |
|
Hi all,
With MathMod 64Bit version, we can reach very hight resolution specs. The 32Bit version is limited due to the memory limitations (4GB maximum) but the 64Bit is only limited by the amount of memory of your machine.
The screen shot shows the MengerSponge at 36Millions triangles obtained with MathMod 64Bit (the goal is a 100Millions triangles with 8GB of RAM):
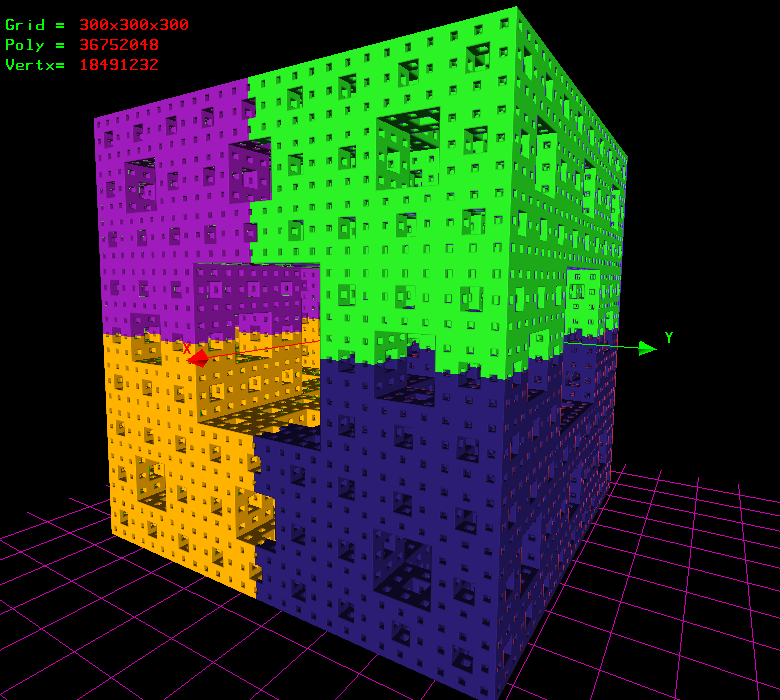 mengersponge by taha_ab, on Flickr mengersponge by taha_ab, on Flickr
Stay tuned 
_________________
Cheers,
Abderrahman |
|
| Back to top |
  |
 |
nextstep
Site Admin
Joined: 06 Jan 2007
Posts: 539
|
 Posted: Thu Jun 05, 2014 4:48 am Post subject: Posted: Thu Jun 05, 2014 4:48 am Post subject: |
 |
|
Hi all,
There are two preloaded scripts of the Menger Sponge model:
MengerSponge and MengerSpongeSubdivision (see below for more informations)
The second script of the Menger Sponge model is a composition of eight components that form the Menger Sponge model and each part is calculated separately from the others, at a default/needed resolution.
So at a resolution R = 100 for example, the MengerSpongeSubdivision script will have a double resolution (i.e R =200) than the normal MengerSponge script. This can be the ultimate solution of calculating high resolution mathematical models with a very low memory footprint. Hope I made myself clear, if not don't hesitate to ask for more details about this great advancement in MathMod 
| Code: | {
"Iso3D": {
"Component": [
"MengerSponge"
],
"Fxyz": [
" -(Dx^100 + Dy^100 + Dz^100 -1)*(((abs(x) >1/3 | abs(y) > 1/3)*(abs(z) >1/3 | abs(y) > 1/3)*(abs(x) >1/3 | abs(z) > 1/3))*( (Cx*(Cy+Cz) + Cz*Cy) =0)*( (Bx*(By+Bz) + Bz*By) =0)*( (Ax*(Ay+Az) + Az*Ay) =0) ) "
],
"Name": [
"MengerSponge"
],
"Varu": [
" A = ((abs(u-2/3) + abs(u-2/3-2/27) + abs(u-2/3+2/27) + abs(u-2/3-2/9) + abs(u-2/3-2/9-2/27) + abs(u-2/3-2/9+2/27) + abs(u-2/3+2/9) + abs(u-2/3+2/9-2/27) + abs(u-2/3+2/9+2/27) + abs(u+2/3) + abs(u+2/3-2/27) + abs(u+2/3+2/27) < 1/81) +(abs(u+2/3-2/9) <1/81) +(abs(u+2/3-2/9-2/27) <1/81) +(abs(u+2/3-2/9+2/27) <1/81) +(abs(u+2/3+2/9) <1/81) +(abs(u+2/3+2/9-2/27) <1/81) +(abs(u+2/3+2/9+2/27) <1/81) +(abs(u) <1/81) + (abs(u-2/27) <1/81) +(abs(u+2/27) <1/81) +(abs(u-2/9) <1/81) + (abs(u-2/9-2/27) <1/81) + (abs(u-2/9+2/27) <1/81) +(abs(u+2/9) <1/81)+(abs(u+2/9-2/27) <1/81)+(abs(u+2/9+2/27) <1/81))",
" B = ((abs(u-2/3) <1/27)+(abs(u-2/3-2/9) <1/27) + (abs(u-2/3+2/9) <1/27) +(abs(u+2/3) <1/27) +(abs(u+2/3-2/9) <1/27) + (abs(u+2/3+2/9) <1/27) +(abs(u) <1/27) + (abs(u-2/9) <1/27) + (abs(u+2/9) <1/27))",
"C = ((abs(u-2/3) <1/9) + (abs(u+2/3) <1/9) + (abs(u) <1/9))",
"D = u^100"
],
"Xmax": [
" 1.001"
],
"Xmin": [
"-1.001"
],
"Ymax": [
" 1.001"
],
"Ymin": [
"-1.001"
],
"Zmax": [
" 1.001"
],
"Zmin": [
"-1.001"
]
}
} |
mengerSpongeSubdivision:
| Code: | {
"Iso3D": {
"Component": [
" MengerSponge1",
" MengerSponge2",
" MengerSponge3",
" MengerSponge4",
" MengerSponge5",
" MengerSponge6",
" MengerSponge7",
" MengerSponge8"
],
"Fxyz": [
" -(Dx^100 + Dy^100 + Dz^100 -1)*(((abs(x) >1/3 | abs(y) > 1/3)*(abs(z) >1/3 | abs(y) > 1/3)*(abs(x) >1/3 | abs(z) > 1/3))*( (Cx*(Cy+Cz) + Cz*Cy) =0)*( (Bx*(By+Bz) + Bz*By) =0)*( (Ax*(Ay+Az) + Az*Ay) =0) ) ",
"-(Dx^100 + Dy^100 + Dz^100 -1)*(((abs(x) >1/3 | abs(y) > 1/3)*(abs(z) >1/3 | abs(y) > 1/3)*(abs(x) >1/3 | abs(z) > 1/3))*( (Cx*(Cy+Cz) + Cz*Cy) =0)*( (Bx*(By+Bz) + Bz*By) =0)*( (Ax*(Ay+Az) + Az*Ay) =0) ) ",
"-(Dx^100 + Dy^100 + Dz^100 -1)*(((abs(x) >1/3 | abs(y) > 1/3)*(abs(z) >1/3 | abs(y) > 1/3)*(abs(x) >1/3 | abs(z) > 1/3))*( (Cx*(Cy+Cz) + Cz*Cy) =0)*( (Bx*(By+Bz) + Bz*By) =0)*( (Ax*(Ay+Az) + Az*Ay) =0) ) ",
"-(Dx^100 + Dy^100 + Dz^100 -1)*(((abs(x) >1/3 | abs(y) > 1/3)*(abs(z) >1/3 | abs(y) > 1/3)*(abs(x) >1/3 | abs(z) > 1/3))*( (Cx*(Cy+Cz) + Cz*Cy) =0)*( (Bx*(By+Bz) + Bz*By) =0)*( (Ax*(Ay+Az) + Az*Ay) =0) )",
"-(Dx^100 + Dy^100 + Dz^100 -1)*(((abs(x) >1/3 | abs(y) > 1/3)*(abs(z) >1/3 | abs(y) > 1/3)*(abs(x) >1/3 | abs(z) > 1/3))*( (Cx*(Cy+Cz) + Cz*Cy) =0)*( (Bx*(By+Bz) + Bz*By) =0)*( (Ax*(Ay+Az) + Az*Ay) =0) ) ",
"-(Dx^100 + Dy^100 + Dz^100 -1)*(((abs(x) >1/3 | abs(y) > 1/3)*(abs(z) >1/3 | abs(y) > 1/3)*(abs(x) >1/3 | abs(z) > 1/3))*( (Cx*(Cy+Cz) + Cz*Cy) =0)*( (Bx*(By+Bz) + Bz*By) =0)*( (Ax*(Ay+Az) + Az*Ay) =0) ) ",
"-(Dx^100 + Dy^100 + Dz^100 -1)*(((abs(x) >1/3 | abs(y) > 1/3)*(abs(z) >1/3 | abs(y) > 1/3)*(abs(x) >1/3 | abs(z) > 1/3))*( (Cx*(Cy+Cz) + Cz*Cy) =0)*( (Bx*(By+Bz) + Bz*By) =0)*( (Ax*(Ay+Az) + Az*Ay) =0) ) ",
"-(Dx^100 + Dy^100 + Dz^100 -1)*(((abs(x) >1/3 | abs(y) > 1/3)*(abs(z) >1/3 | abs(y) > 1/3)*(abs(x) >1/3 | abs(z) > 1/3))*( (Cx*(Cy+Cz) + Cz*Cy) =0)*( (Bx*(By+Bz) + Bz*By) =0)*( (Ax*(Ay+Az) + Az*Ay) =0) )"
],
"Name": [
"MengerSpongeSubdivision"
],
"Varu": [
" A = ((abs(u-2/3) <1/81)+ (abs(u-20/27) <1/81)+ (abs(u-16/27) <1/81)+(abs(u-8/9) <1/81) + (abs(u-26/27) <1/81) + (abs(u-22/27) <1/81) +(abs(u-4/9) <1/81) +(abs(u-14/27) <1/81) +(abs(u-10/27) <1/81) +(abs(u+2/3) <1/81) +(abs(u+16/27) <1/81) +(abs(u+20/27) <1/81) +(abs(u+4/9) <1/81) +(abs(u+10/27) <1/81) +(abs(u+14/27) <1/81) +(abs(u+8/9) <1/81) +(abs(u+22/27) <1/81) +(abs(u+26/27) <1/81) +(abs(u) <1/81) + (abs(u-2/27) <1/81) +(abs(u+2/27) <1/81) +(abs(u-2/9) <1/81) + (abs(u-8/27) <1/81) + (abs(u-4/27) <1/81) +(abs(u+2/9) <1/81)+(abs(u+4/27) <1/81)+(abs(u+8/27) <1/81))",
" B = ((abs(u-2/3) <1/27)+(abs(u-8/9) <1/27) + (abs(u-4/9) <1/27) +(abs(u+2/3) <1/27) +(abs(u+4/9) <1/27) + (abs(u+8/9) <1/27) +(abs(u) <1/27) + (abs(u-2/9) <1/27) + (abs(u+2/9) <1/27))",
"C = ((abs(u-2/3) <1/9) + (abs(u+2/3) <1/9) + (abs(u) <1/9))",
"D = u^100"
],
"Xmax": [
" 0.000 ",
" 0.000",
" 0.000",
" 0.000",
" 1.001",
" 1.001",
" 1.001",
" 1.001"
],
"Xmin": [
"-1.001",
" -1.001 ",
" -1.001",
" -1.001",
" 0.000",
" 0.000",
" 0.000",
" 0.000"
],
"Ymax": [
" 0.000 ",
" 0.000",
" 1.001",
" 1.001",
" 0.000 ",
" 0.000",
" 1.001",
" 1.001"
],
"Ymin": [
"-1.001",
" -1.001",
" 0.000",
" 0.000",
" -1.001",
" -1.001",
" 0.000",
" 0.000 "
],
"Zmax": [
" 0.000 ",
" 1.001",
" 0.000",
" 1.001",
" 0.000 ",
" 1.001",
" 0.000",
" 1.001"
],
"Zmin": [
"-1.001",
" 0.000 ",
" -1.001",
" 0.000",
" -1.001",
" 0.000 ",
" -1.001",
" 0.000 "
]
}
}
|
_________________
Cheers,
Abderrahman |
|
| Back to top |
  |
 |
nextstep
Site Admin
Joined: 06 Jan 2007
Posts: 539
|
 Posted: Fri Jun 13, 2014 1:46 am Post subject: Posted: Fri Jun 13, 2014 1:46 am Post subject: |
 |
|
Hi all,
I discovered that the MengerSponge formulas included in the mathmodcollection.js isn't accurate and doesn't reflect the original version that I posted the 12 Sep 2007 ! That's weird because they looked the same at heigh resolution...
I'm I sad? no, why? because the original one version shows so beautiful results even at low grid resolution 
The original version
| Quote: |
if(( abs(x) >1/3 | abs(y) > 1/3 ) &( abs(z) >1/3 | abs(y) > 1/3 ) &( abs(x) >1/3 | abs(z) > 1/3 )
&
( (( ( (abs(x-2/3) <1/9) + (abs(x+2/3) <1/9) + (abs(x) <1/9) ) * ((abs(y-2/3) < 1/9) +(abs(y) < 1/9) +(abs(y+2/3) <1/9) + (abs(z-2/3) < 1/9) +(abs(z) < 1/9) + (abs(z+2/3) < 1/9))) +( ( (abs(z-2/3) <1/9) + (abs(z+2/3) <1/9) + (abs(z) <1/9) ) * ( (abs(y-2/3) < 1/9) + (abs(y) < 1/9) + (abs(y+2/3) < 1/9))) ) =0)
&
( (( ( (abs(x-2/3) <1/27)+(abs(x-2/3-2/9) <1/27) + (abs(x-2/3+2/9) <1/27) +(abs(x+2/3) <1/27) +(abs(x+2/3-2/9) <1/27) + (abs(x+2/3+2/9) <1/27) +(abs(x) <1/27) + (abs(x-2/9) <1/27) + (abs(x+2/9) <1/27)) * ((abs(y-2/3) < 1/27) + (abs(y-2/3-2/9) < 1/27) + (abs(y-2/3+2/9) < 1/27) +(abs(y) < 1/27) + (abs(y-2/9) < 1/27) + (abs(y+2/9) < 1/27) + (abs(y+2/3) <1/27) + (abs(y+2/3-2/9) <1/27) + (abs(y+2/3+2/9) <1/27) + (abs(z-2/3) < 1/27) + (abs(z-2/3-2/9) < 1/27) + (abs(z-2/3+2/9) < 1/27) + (abs(z) < 1/27) + (abs(z-2/9) < 1/27) + (abs(z+2/9) < 1/27) + (abs(z+2/3) < 1/27) + (abs(z+2/3-2/9) < 1/27) + (abs(z+2/3+2/9) < 1/27) )) +( ( (abs(z-2/3) <1/27) + (abs(z-2/3-2/9) <1/27) + (abs(z-2/3+2/9) <1/27) + (abs(z+2/3) <1/27) + (abs(z+2/3-2/9) <1/27) + (abs(z+2/3+2/9) <1/27) + (abs(z) <1/27) + (abs(z-2/9) <1/27) + (abs(z+2/9) <1/27) ) * ( (abs(y-2/3) < 1/27) + (abs(y-2/3-2/9) < 1/27) + (abs(y-2/3+2/9) < 1/27) + (abs(y) < 1/27) + (abs(y-2/9) < 1/27) + (abs(y+2/9) < 1/27) + (abs(y+2/3) < 1/27) + (abs(y+2/3-2/9) < 1/27) + (abs(y+2/3+2/9) < 1/27)))) =0)
&
( ((
(
(abs(x-2/3) <1/81)+ (abs(x-2/3-2/27) <1/81)+ (abs(x-2/3+2/27) <1/81)+
(abs(x-2/3-2/9) <1/81) + (abs(x-2/3-2/9-2/27) <1/81) + (abs(x-2/3-2/9+2/27) <1/81) +
(abs(x-2/3+2/9) <1/81) +(abs(x-2/3+2/9-2/27) <1/81) +(abs(x-2/3+2/9+2/27) <1/81) +
(abs(x+2/3) <1/81) +(abs(x+2/3-2/27) <1/81) +(abs(x+2/3+2/27) <1/81) +
(abs(x+2/3-2/9) <1/81) +(abs(x+2/3-2/9-2/27) <1/81) +(abs(x+2/3-2/9+2/27) <1/81) +
(abs(x+2/3+2/9) <1/81) +(abs(x+2/3+2/9-2/27) <1/81) +(abs(x+2/3+2/9+2/27) <1/81) +
(abs(x) <1/81) + (abs(x-2/27) <1/81) +(abs(x+2/27) <1/81) +
(abs(x-2/9) <1/81) + (abs(x-2/9-2/27) <1/81) + (abs(x-2/9+2/27) <1/81) +
(abs(x+2/9) <1/81)+(abs(x+2/9-2/27) <1/81)+(abs(x+2/9+2/27) <1/81)
) *
(
(abs(y-2/3) < 1/81) + (abs(y-2/3-2/27) < 1/81) +(abs(y-2/3+2/27) < 1/81) +
(abs(y-2/3-2/9) < 1/81) + (abs(y-2/3-2/9-2/27) < 1/81) +(abs(y-2/3-2/9+2/27) < 1/81) +
(abs(y-2/3+2/9) < 1/81) +(abs(y-2/3+2/9-2/27) < 1/81) +(abs(y-2/3+2/9+2/27) < 1/81) +
(abs(y) < 1/81) + (abs(y-2/27) < 1/81) + (abs(y+2/27) < 1/81) +
(abs(y-2/9) < 1/81) + (abs(y-2/9-2/27) < 1/81) + (abs(y-2/9+2/27) < 1/81) +
(abs(y+2/9) < 1/81) + (abs(y+2/9-2/27) < 1/81) + (abs(y+2/9+2/27) < 1/81) +
(abs(y+2/3) <1/81) + (abs(y+2/3-2/27) <1/81) + (abs(y+2/3+2/27) <1/81) +
(abs(y+2/3-2/9) <1/81) + (abs(y+2/3-2/9-2/27) <1/81) + (abs(y+2/3-2/9+2/27) <1/81) +
(abs(y+2/3+2/9) <1/81) + (abs(y+2/3+2/9-2/27) <1/81) + (abs(y+2/3+2/9+2/27) <1/81) +
(abs(z-2/3) < 1/81) + (abs(z-2/3-2/27) < 1/81) + (abs(z-2/3+2/27) < 1/81) +
(abs(z-2/3-2/9) < 1/81) + (abs(z-2/3-2/9-2/27) < 1/81) + (abs(z-2/3-2/9+2/27) < 1/81) +
(abs(z-2/3+2/9) < 1/81) + (abs(z-2/3+2/9-2/27) < 1/81) + (abs(z-2/3+2/9+2/27) < 1/81) +
(abs(z) < 1/81) + (abs(z-2/27) < 1/81) + (abs(z+2/27) < 1/81) +
(abs(z-2/9) < 1/81) + (abs(z-2/9-2/27) < 1/81) + (abs(z-2/9+2/27) < 1/81) +
(abs(z+2/9) < 1/81) + (abs(z+2/9-2/27) < 1/81) + (abs(z+2/9+2/27) < 1/81) +
(abs(z+2/3) < 1/81) + (abs(z+2/3-2/27) < 1/81) + (abs(z+2/3+2/27) < 1/81) +
(abs(z+2/3-2/9) < 1/81) + (abs(z+2/3-2/9-2/27) < 1/81) + (abs(z+2/3-2/9+2/27) < 1/81) +
(abs(z+2/3+2/9) < 1/81) +(abs(z+2/3+2/9-2/27) < 1/81) +(abs(z+2/3+2/9+2/27) < 1/81)
)) +
(
(
(abs(z-2/3) <1/81) + (abs(z-2/3-2/27) <1/81) + (abs(z-2/3+2/27) <1/81) +
(abs(z-2/3-2/9) <1/81) + (abs(z-2/3-2/9-2/27) <1/81) + (abs(z-2/3-2/9+2/27) <1/81) +
(abs(z-2/3+2/9) <1/81) + (abs(z-2/3+2/9-2/27) <1/81) + (abs(z-2/3+2/9+2/27) <1/81) +
(abs(z+2/3) <1/81) + (abs(z+2/3-2/27) <1/81) + (abs(z+2/3+2/27) <1/81) +
(abs(z+2/3-2/9) <1/81) + (abs(z+2/3-2/9-2/27) <1/81) + (abs(z+2/3-2/9+2/27) <1/81) +
(abs(z+2/3+2/9) <1/81) + (abs(z+2/3+2/9-2/27) <1/81) + (abs(z+2/3+2/9+2/27) <1/81) +
(abs(z) <1/81) + (abs(z-2/27) <1/81) + (abs(z+2/27) <1/81) +
(abs(z-2/9) <1/81) + (abs(z-2/9-2/27) <1/81) + (abs(z-2/9+2/27) <1/81) +
(abs(z+2/9) <1/81) + (abs(z+2/9-2/27) <1/81) + (abs(z+2/9+2/27) <1/81)
) * (
(abs(y-2/3) < 1/81) + (abs(y-2/3-2/27) < 1/81) + (abs(y-2/3+2/27) < 1/81) +
(abs(y-2/3-2/9) < 1/81) + (abs(y-2/3-2/9-2/27) < 1/81) + (abs(y-2/3-2/9+2/27) < 1/81) +
(abs(y-2/3+2/9) < 1/81) + (abs(y-2/3+2/9-2/27) < 1/81) + (abs(y-2/3+2/9+2/27) < 1/81) +
(abs(y) < 1/81) + (abs(y-2/27) < 1/81) + (abs(y+2/27) < 1/81) +
(abs(y-2/9) < 1/81) + (abs(y-2/9-2/27) < 1/81) + (abs(y-2/9+2/27) < 1/81) +
(abs(y+2/9) < 1/81) + (abs(y+2/9-2/27) < 1/81) + (abs(y+2/9+2/27) < 1/81) +
(abs(y+2/3) < 1/81) + (abs(y+2/3-2/27) < 1/81) + (abs(y+2/3+2/27) < 1/81) +
(abs(y+2/3-2/9) < 1/81) + (abs(y+2/3-2/9-2/27) < 1/81) + (abs(y+2/3-2/9+2/27) < 1/81) +
(abs(y+2/3+2/9) < 1/81) + (abs(y+2/3+2/9-2/27) < 1/81) + (abs(y+2/3+2/9+2/27) < 1/81)
)
)) =0)
|
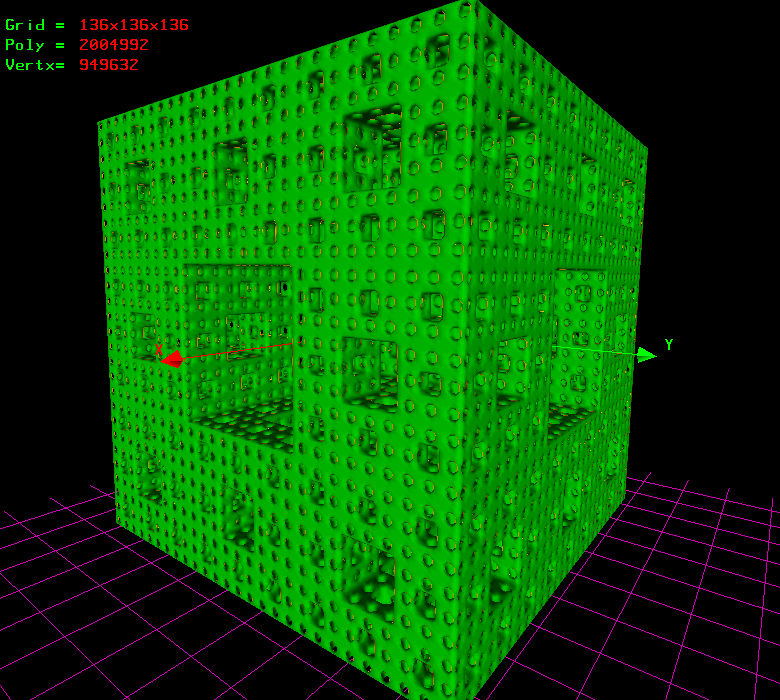 MengerSpongeOrigine by taha_ab, on Flickr MengerSpongeOrigine by taha_ab, on Flickr
_________________
Cheers,
Abderrahman |
|
| Back to top |
  |
 |
nextstep
Site Admin
Joined: 06 Jan 2007
Posts: 539
|
 Posted: Fri Jul 04, 2014 12:00 am Post subject: Posted: Fri Jul 04, 2014 12:00 am Post subject: |
 |
|
Hi all,
In a previous message, I said:
| Quote: | | The screen shot shows the MengerSponge at 36Millions triangles obtained with MathMod 64Bit (the goal is a 100Millions triangles with 8GB of RAM) |
The goal of 100millions triangles has just been break down (145 Millions triangles)...
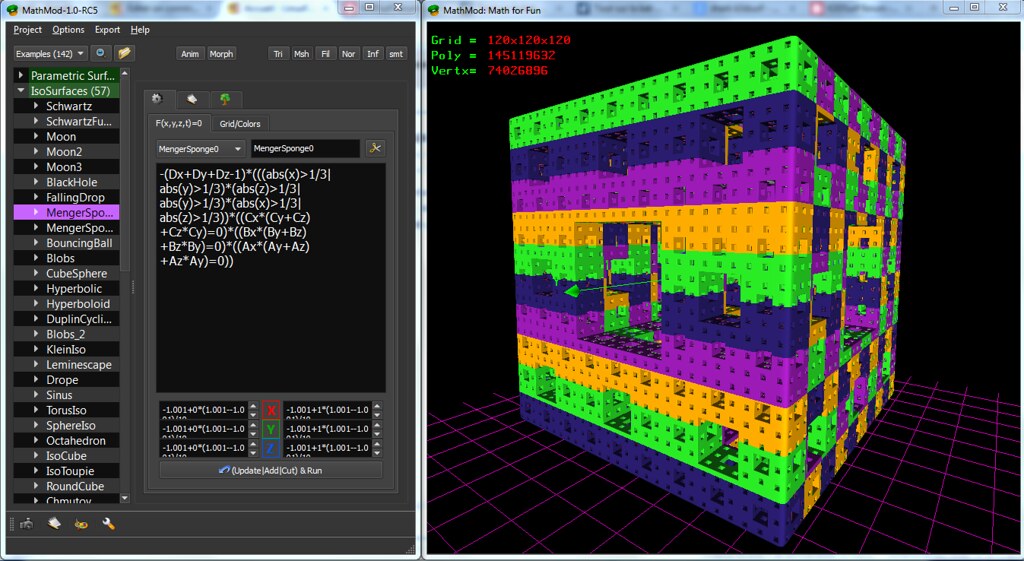 MengerSponge145 by taha_ab, on Flickr MengerSponge145 by taha_ab, on Flickr
_________________
Cheers,
Abderrahman |
|
| Back to top |
  |
 |
nextstep
Site Admin
Joined: 06 Jan 2007
Posts: 539
|
 Posted: Sat Jul 05, 2014 12:41 am Post subject: Posted: Sat Jul 05, 2014 12:41 am Post subject: |
 |
|
Hi,
Some of you might ask : how can it be that with only a grid of 120x120x120, a MengerSponge can go to 145Millions triangles?
The answer is that the number of triangles generated by a scripted mathematical model is the sum of the number of triangles of each component included in the script and each component is calculated with a resolution of 120x120x120.
The script I used to calculate the MengerSponge has 1000 components and each component is a small part of the entire MengerSponge model.
The final result is then equivalent to a MengerSponge calculated with a grid of 1200x1200x1200! That's quite a huge grid and don't expect to be able to set such a grid with MathMod any soon, unless you have 1 Tera of RAM 
This is, I think, a good solution to bypass the huge amount of RAM needed to calculate a hight resolution models.
The script of 1000 components I used was generated by a new tool that will be included in MathMod.
Stay tuned 
_________________
Cheers,
Abderrahman |
|
| Back to top |
  |
 |
|
|
You cannot post new topics in this forum
You cannot reply to topics in this forum
You cannot edit your posts in this forum
You cannot delete your posts in this forum
You cannot vote in polls in this forum
|
2005 Powered by phpBB © 2001, 2005 phpBB Group
|