|
| View previous topic :: View next topic |
| Author |
Message |
nextstep
Site Admin
Joined: 06 Jan 2007
Posts: 539
|
 Posted: Fri Sep 05, 2014 4:28 am Post subject: Endraß octic (deg 8) Posted: Fri Sep 05, 2014 4:28 am Post subject: Endraß octic (deg 8) |
 |
|
Hi all,
Endraß surfaces are a pair of octic surfaces which have 168 ordinary double points. This is the maximum number known to exist for an octic surface, although the rigorous upper bound is 174.
Endraß constructed it in 1997 during the writing of his Ph.D. thesis (advisor W. Barth).
The surfaces were discovered in a five-dimensional family of octics with 112 nodes.
The illustrated surface take w=1 and has 144 real ordinary double points.
| Code: | {
"Iso3D": {
"Cnd": [
"(x^2+y^2+z^2)>25"
],
"Component": [
"Endraß-Octic"
],
"Const": [
" w = 1.0",
"a1 = 1.0",
"a2 = 1.0",
"a3 = 1.0",
"a4 = -1.0"
],
"Fxyz": [
"64 * (x^2 - w^2)*(y^2 - w^2)*((x + y)^2 -2*w^2)*((x - y)^2 -2*w^2) - (-4*(1 + a1*2^(1/2))*(x^2 + y^2)^2 +
(8*(2 + a2*2^(1/2))*z^2 + 2*(2 + a3*7*2^(1/2))*w^2 )* (x^2 + y^2) -
16*z^4+ 8*(1 + a4*2*2^(1/2))*z^2*w^2 - (1 + 12*2^(1/2))*w^4)^2"
],
"Name": [
"Endraß-Octic"
],
"Xmax": [
"5"
],
"Xmin": [
"-5"
],
"Ymax": [
"5"
],
"Ymin": [
"-5"
],
"Zmax": [
"5"
],
"Zmin": [
"-5"
]
}
} |
 EndraßOctic by taha_ab, on Flickr EndraßOctic by taha_ab, on Flickr
_________________
Cheers,
Abderrahman |
|
| Back to top |
  |
 |
nextstep
Site Admin
Joined: 06 Jan 2007
Posts: 539
|
 Posted: Sat Sep 20, 2014 11:28 pm Post subject: Sarti's Octic Posted: Sat Sep 20, 2014 11:28 pm Post subject: Sarti's Octic |
 |
|
Hi all,
This is the Alessandra Sarti's Octic version with 144 nodes (see also her Dodecic (deg 12) 600 nodes)
| Quote: | {
"Iso3D": {
"Component": [
" SartiOctic"
],
"Fxyz": [
"-1728*x^4*y^2*z^2+928.0*z^4*x^4+9024.0*z^2*x^4+928.0*z^4*y^4+9024.0*z^2*y^4+9024.0*x^2*y^2+2720.0*x^4*y^4-1728*x^2*z^2-1728*y^2*z^2-1728*x^4*y^2-1728*x^2*y^4-1728*x^2*z^4-1728*y^2*z^4-576*x^6*y^2-576*x^6*z^2-576*x^2*y^6-576*x^2*z^6-576*y^6*z^2+9024.0*z^4*x^2*y^2-24960.0*z^2*x^2*y^2-1728*x^2*y^4*z^2+2720.0*z^4+112.0*z^8-576*z^2+928.0*x^4+112.0*x^8+928.0*y^4+112.0*y^8-576*x^2-576*y^2-576*x^6-576*y^6-576*z^6+112.0-576*y^2*z^6"
],
"Name": [
"SartiOctic"
],
"Xmax": [
"5.6"
],
"Xmin": [
"-5.6"
],
"Ymax": [
"5.6"
],
"Ymin": [
"-5.6"
],
"Zmax": [
"5.6"
],
"Zmin": [
"-5.6"
]
}
}
|
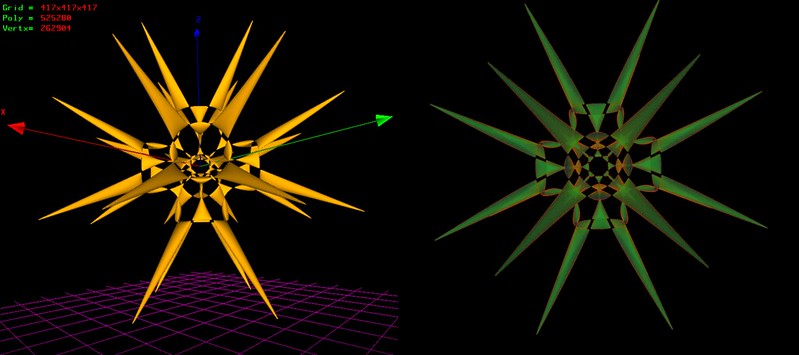 SartiOctic by taha_ab, on Flickr SartiOctic by taha_ab, on Flickr
_________________
Cheers,
Abderrahman |
|
| Back to top |
  |
 |
|
|
You cannot post new topics in this forum
You cannot reply to topics in this forum
You cannot edit your posts in this forum
You cannot delete your posts in this forum
You cannot vote in polls in this forum
|
2005 Powered by phpBB © 2001, 2005 phpBB Group
|