|
| View previous topic :: View next topic |
| Author |
Message |
nextstep
Site Admin
Joined: 06 Jan 2007
Posts: 539
|
 Posted: Mon Sep 01, 2014 11:42 pm Post subject: Barth Sextic (deg 6) Posted: Mon Sep 01, 2014 11:42 pm Post subject: Barth Sextic (deg 6) |
 |
|
Hi all,
The Barth-sextic is a sextic surface in complex three-dimensional projective space having the maximum possible number of ordinary double points, namely 65. The surface was discovered by W. Barth in 1994, and is given by the implicit equation
4(phi^2x^2-y^2)(phi^2y^2-z^2)(phi^2z^2-x^2)-(1+2phi)(x^2+y^2+z^2-w^2)^2w^2=0.
where phi is the golden ratio.
Barth's sextic surface has 65 double points: Of these, 20 nodes are at the vertices of a regular dodecahedron of side length 2/phi and circumradius sqrt(3) ,30 are at the vertices of a concentric icosidodecahedron and circumradius 1 and 15 of the nodes are at infinity.
| Quote: | {
"Iso3D": {
"Cnd": [
"(x^2+y^2+z^2)>9"
],
"Component": [
"Barth-sextic"
],
"Const": [
" w=1.0",
" phi=(1/2)*(1+sqrt(5))"
],
"Fxyz": [
"4*(phi^2*x^2-y^2)*(phi^2*y^2-z^2)*(phi^2*z^2-x^2)-(1+2*phi)*(x^2+y^2+z^2-w^2)^2*w^2"
],
"Name": [
"Barth-sextic"
],
"Xmax": [
"3"
],
"Xmin": [
"-3"
],
"Ymax": [
"3"
],
"Ymin": [
"-3"
],
"Zmax": [
"3"
],
"Zmin": [
"-3"
]
}
} |
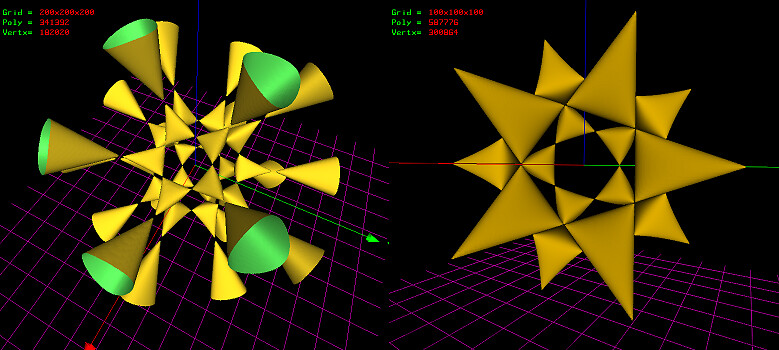 BarthSextic by taha_ab, on Flickr BarthSextic by taha_ab, on Flickr
_________________
Cheers,
Abderrahman
Last edited by nextstep on Sat Sep 20, 2014 5:43 pm; edited 1 time in total |
|
| Back to top |
  |
 |
inode

Joined: 27 Jan 2007
Posts: 127
Location: Austria
|
 Posted: Tue Sep 02, 2014 8:09 am Post subject: formula data formating Posted: Tue Sep 02, 2014 8:09 am Post subject: formula data formating |
 |
|
Hi Abderrahman
Thank you for publishing those basics about algebraic surfaces!
What strikes me is that the formula parameter presentation is not clearly arranged. More clearly would be to format it like this...
| Quote: | {
"Iso3D":
{
"Cnd": [ "(x^2+y^2+z^2)>9" ],
"Component": [ "Barth-sextic" ],
"Const": [ " w=1.0", " phi=(1/2)*(1+sqrt(5))" ],
"Fxyz": [ "4*(phi^2*x^2-y^2)*(phi^2*y^2-z^2)*(phi^2*z^2-x^2)-(1+2*phi)*(x^2+y^2+z^2-w^2)^2*w^2" ],
"Name": [ "Barth-sextic" ],
"Xmax": [ "3" ],
"Xmin": [ "-3" ],
"Ymax": [ "3" ],
"Ymin": [ "-3" ],
"Zmax": [ "3" ],
"Zmin": [ "-3" ]
}
} |
Do you think that this is possible?
Range values would also be more readable if they are coded like K3dSurf...
"x": [3, -3]
"y": [3, -3]
"z": [3, -3]
Whatever, you know that is only a consideration.
 Gerd Gerd |
|
| Back to top |
  |
 |
nextstep
Site Admin
Joined: 06 Jan 2007
Posts: 539
|
 Posted: Wed Sep 03, 2014 1:12 am Post subject: Posted: Wed Sep 03, 2014 1:12 am Post subject: |
 |
|
Hi Gerd,
You're right but, as far as I know, it's not possible to achieve that with the actual JSON Support in Qt. Hope this feature will be supported soon.
| Code: | Range values would also be more readable if they are coded like K3dSurf...
"x": [3, -3]
"y": [3, -3]
"z": [3, -3] |
MathMod's scripts targets mathematical models with high number of components, and unfortunately, this rearrangement will not help when playing with high number of components...I'm more and more using MathMod to read and modify my scripts and I'll add new ways to make the editing easier.
_________________
Cheers,
Abderrahman |
|
| Back to top |
  |
 |
nextstep
Site Admin
Joined: 06 Jan 2007
Posts: 539
|
 Posted: Sat Sep 20, 2014 4:26 am Post subject: Boy surface Posted: Sat Sep 20, 2014 4:26 am Post subject: Boy surface |
 |
|
Hi all,
Boy's surface, found by Werner Boy in 1901, is an immersion of the real projective plane in 3-dimensional space.
Boy's surface is discussed (and illustrated) in Jean-Pierre Petit's Le Topologicon.
Boy's surface was first parametrized explicitly by Bernard Morin in 1978.
Boy's surface has 3-fold symmetry. This means that it has an axis of discrete rotational symmetry: any 120° turn about this axis will leave the surface looking exactly the same. The Boy's surface can be cut into three mutually congruent pieces.
The Boy surface is a model of the projective plane without singularities and is a sextic surface.
| Quote: | {
"Param3D": {
"Name": [
"Boy"
],
"Component": [
"Boy"
],
"Fx": [
"2/3*(cos(u)*cos(2*v)+sqrt(2)*sin(u)*cos(v))*cos(u)/(sqrt(2)-sin(2*u)*sin(3*v))"
],
"Fy": [
"2/3*(cos(u)*sin(2*v)-sqrt(2)*sin(u)*sin(v))*cos(u)/(sqrt(2)-sin(2*u)*sin(3*v))"
],
"Fz": [
"sqrt(2)*cos(u)*cos(u)/(sqrt(2)-sin(2*u)*sin(3*v))"
],
"Umax": [
"pi"
],
"Umin": [
"0"
],
"Vmax": [
"pi"
],
"Vmin": [
"0"
]
}
}
|
 Boy by taha_ab, on Flickr Boy by taha_ab, on Flickr
_________________
Cheers,
Abderrahman |
|
| Back to top |
  |
 |
inode

Joined: 27 Jan 2007
Posts: 127
Location: Austria
|
 Posted: Tue Sep 30, 2014 9:32 am Post subject: another representation ... Posted: Tue Sep 30, 2014 9:32 am Post subject: another representation ... |
 |
|
Hi all
More infos about Boy's surface(s) you'll get at ...
http://www.math.smith.edu/~patela/boysurface/AmyJenny/other_boys.html
E.g. this is another representation of Boy's surface as an algebraic surface ...
| Code: | Name: rs_Boy1
/* Isosurface: rs_Boy1 10/2013 RealSurf
http://realsurf.informatik.uni-halle.de/
http://www.singsurf.org/singsurf/SingSurf.html
*/
F(): 64*(1-z)^3*z^3
- 48*(1-z)^2*z^2*(3*x^2 +3*y^2 +2*z^2)
+ 12*(1-z)*z*( 27*(x^2 +y^2)^2
-24*z^2*(x^2 +y^2)
+36*sqrt(2)*y*z*(y^2 -3*x^2)
+4*z^4
)
+ (9*x^2 +9*y^2 -2*z^2)
* (-81*(x^2 +y^2)^2
-72*z^2*(x^2 +y^2)
+108*sqrt(2)*x*z*(x^2 -3*y^2) +4*z^4
)
[x]: -1 , 1.5
[y]: -1.4 , 1.2
[z]: 0 , 2
; |
ps. Abderrahman, shouldn't this be a seperate posting for a 'BOY surface'? |
|
| Back to top |
  |
 |
nextstep
Site Admin
Joined: 06 Jan 2007
Posts: 539
|
 Posted: Thu Oct 02, 2014 11:44 pm Post subject: Posted: Thu Oct 02, 2014 11:44 pm Post subject: |
 |
|
Hi Gerd,
| Quote: | | ps. Abderrahman, shouldn't this be a seperate posting for a 'BOY surface'? |
Sorry I completely forget to respond...
It's there only because it's also a sextic surface but you can open a new thread if you wish : Boy's surface actually is worth more than one thread

_________________
Cheers,
Abderrahman |
|
| Back to top |
  |
 |
|
|
You cannot post new topics in this forum
You cannot reply to topics in this forum
You cannot edit your posts in this forum
You cannot delete your posts in this forum
You cannot vote in polls in this forum
|
2005 Powered by phpBB © 2001, 2005 phpBB Group
|