|
| View previous topic :: View next topic |
| Author |
Message |
nextstep
Site Admin
Joined: 06 Jan 2007
Posts: 539
|
 Posted: Mon Sep 01, 2014 2:41 am Post subject: Togliatti quintic (deg 5) Posted: Mon Sep 01, 2014 2:41 am Post subject: Togliatti quintic (deg 5) |
 |
|
Togliatti (1940, 1949) showed that quintic surfaces having 31 ordinary double points exist, although he did not explicitly derive equations for such surfaces. Beauville (1978) subsequently proved that 31 double points are the maximum possible, and quintic surfaces having 31 ordinary double points are therefore sometimes called Togliatti surfaces. van Straten (1993) subsequently constructed a three-dimensional family of solutions and in 1994, Barth derived the example
| Quote: | 64(x-w)[x^4-4x^3w-10x^2y^2-4x^2w^2+16xw^3-20xy^2w+5y^4+16w^4-20y^2w^2]
-5sqrt(5-sqrt(5))(2z-sqrt(5-sqrt(5))w)[4(x^2+y^2+z^2)+(1+3sqrt(5))w^2]^2,
where w is a parameter (Endraß 2003). |
This surface is invariant under the group D_5 and contains exactly 15 lines. Five of these are the intersection of the surface with a D_5-invariant cone containing 16 nodes, five are the intersection of the surface with a D_5-invariant plane containing 10 nodes, and the last five are the intersection of the surface with a second D_5-invariant plane containing no nodes (Endraß 2003).
In MathMod:
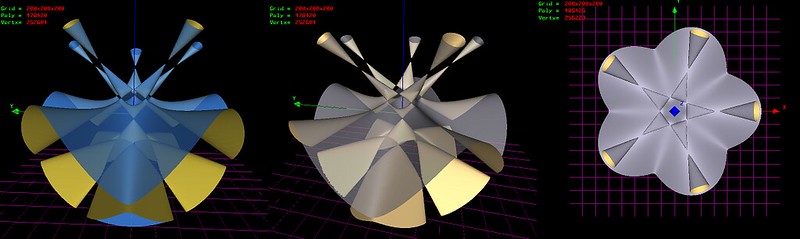 TogliattiQuintics by taha_ab, on Flickr TogliattiQuintics by taha_ab, on Flickr
| Quote: | {
"Iso3D": {
"Cnd": [
"(x^2 + y^2 + z^2) > 100"
],
"Component": [
"Togliatti"
],
"Const": [
" w=1.3"
],
"Fxyz": [
"64*(x -w)*(x^4 - 4*w*x^3 -1 0*x^2*y^2 - 4*x^2*w^2 + 16*w^3*x - 20*w*x*y^2 + 5*y^4 + 16*w^4 - 20*y^2*w^2) -5*sqrt(5 - sqrt(5))*(2*z - sqrt(5 - sqrt(5))*w)*(4*(x^2 + y^2 - z^2) + (1 + 3*sqrt(5))*w^2)^2"
],
"Name": [
"Togliatti"
],
"Xmax": [
"10"
],
"Xmin": [
"-10"
],
"Ymax": [
"10"
],
"Ymin": [
"-10"
],
"Zmax": [
"10"
],
"Zmin": [
"-10"
]
}
}
|
_________________
Cheers,
Abderrahman
Last edited by nextstep on Sat Sep 20, 2014 5:44 pm; edited 1 time in total |
|
| Back to top |
  |
 |
nextstep
Site Admin
Joined: 06 Jan 2007
Posts: 539
|
 Posted: Sat Sep 13, 2014 6:11 pm Post subject: Posted: Sat Sep 13, 2014 6:11 pm Post subject: |
 |
|
Hi,
Another Togliatti related surface, sometimes known as the "Dervish", can be defined by the MathMod's script :
| Quote: |
{
"Iso3D": {
"Name": [
"Dervish"
],
"Component": [
" Dervish"
],
"Cnd": [
"(x^2+y^2+z^2)>15"
],
"Const": [
"r = (1/4)*(1+3*sqrt(5))",
"a = -(8/5)*(1+1/(sqrt(5)))*sqrt(5-sqrt(5))",
"c = (1/2)*sqrt(5-sqrt(5))"
],
"Fxyz": [
"a*(x-z)*(cos((2*pi)/5)*x-sin((2*pi)/5)*y-z)*(cos((4*pi)/5)*x-sin((4*pi)/5)*y-z)*(cos((6*pi)/5)*x-sin((6*pi)/5)*y-z)*(cos((8*pi)/5)*x-sin((8*pi)/5)*y-z)+(1-c*z)*(x^2+y^2-1+r*z^2)^2"
],
"Xmax": [
"4"
],
"Xmin": [
"-4"
],
"Ymax": [
"4"
],
"Ymin": [
"-4"
],
"Zmax": [
"4"
],
"Zmin": [
"-4"
]
}
}
|
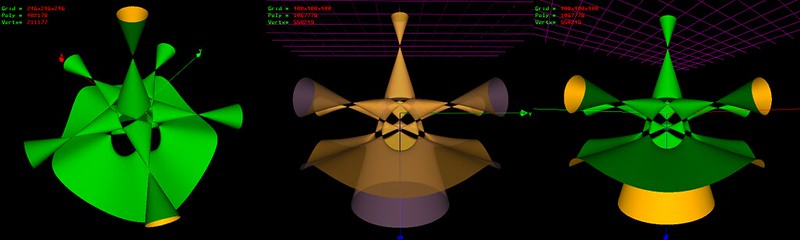 Dervish by taha_ab, on Flickr Dervish by taha_ab, on Flickr
_________________
Cheers,
Abderrahman |
|
| Back to top |
  |
 |
|
|
You cannot post new topics in this forum
You cannot reply to topics in this forum
You cannot edit your posts in this forum
You cannot delete your posts in this forum
You cannot vote in polls in this forum
|
2005 Powered by phpBB © 2001, 2005 phpBB Group
|